D
分析:由ABCD为平行四边形,得到对边AD与BG平行,根据两直线平行内错角相等,得到两对内错角相等,根据两对对应角相等的两三角形相似可得出三角形AEH与三角形GBH相似;再由平行四边形的对边平行得到FC与AB平行,根据两直线平行同位角相等得到两对同位角相等,根据两对对应角相等的两三角形相似可得出三角形GCF与三角形GBA相似;由AD平行于CG,得到两对内错角相等,根据两对对应角相等的两三角形相似可得出三角形ADF与三角形FCG相似;由平行四边形的对角相等得到一对角相等,再由AD与BG平行得到一对内错角相等,根据两对对应角相等的两三角形相似可得出三角形ADF与三角形ABG相似,综上,得到图形中有4对相似三角形.
解答:图中相似的三角形有4对:△AEH∽GBH;△GCF∽△GBA;△ADF∽△GCF;△ADF∽△GBA,
理由如下:
∵四边形ABCD为平行四边形,
∴AD∥BG,
∴∠EAH=∠G,∠AEH=∠HBG,
∴△AEH∽△GBC;
∵四边形ABCD为平行四边形,
∴FC∥AB,
∴∠GFC=∠GAB,∠GCF=∠GBA,
∴△GCF∽△GBA;
∵AD∥BG,
∴∠DAF=∠G,∠D=∠FCG,
∴△ADF∽△GCF;
∵四边形ABCD为平行四边形,
∴∠ABC=∠D,又∠DAF=∠G,
∴△ADF∽△GBA,
综上,图中相似三角形有4对.
故选D
点评:此题考查了相似三角形的判定,平行线的性质,以及平行四边形的性质,其中相似三角形的判定方法有:两对对应角相等的两三角形相似;两边对应成比例且夹角相等的两三角形相似;三边对应成比例的两三角形相似.

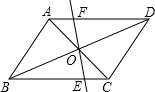
 如图,?ABCD中,E、F分别是AD、CD边的中点,连接AF交BC的延长线于G,连接BE交AF于H,则图中相似的三角形有
如图,?ABCD中,E、F分别是AD、CD边的中点,连接AF交BC的延长线于G,连接BE交AF于H,则图中相似的三角形有

 如图,?ABCD中,AB⊥AC,AB=1,BC=
如图,?ABCD中,AB⊥AC,AB=1,BC=