
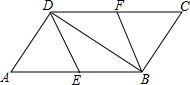
 如图,在?ABCD中,E、F分别为边AB、CD的中点,连接DE、BF、BD.
如图,在?ABCD中,E、F分别为边AB、CD的中点,连接DE、BF、BD.分析 (1)根据平行四边形的性质可得∠A=∠C,AD=BC,CD=AB,进而可得CF=AE,然后利用SAS定理判定△ADE≌△CBF;
(2)首先证明四边形ABCD是平行四边形,再根据直角三角形的性质可得DE=EB,根据邻边相等的平行四边形是菱形可得结论.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴∠A=∠C,AD=BC,CD=AB,
∵E、F分别为边AB、CD的中点,
∴CF=AE,
在△ADE和△CBF中,
$\left\{\begin{array}{l}{AD=BC}\\{∠A=∠C}\\{AE=FC}\end{array}\right.$,
∴△ADE≌△CBF(SAS);
(2)解:菱形,
∵△ADE≌△CBF,
∴ED=BF,
∵DF=EB,
∴四边形ABCD是平行四边形,
∵AD⊥BD,E为边AB中点,
∴DE=$\frac{1}{2}$AB,
∴DE=EB,
∴四边形BFDE是菱形.
点评 此题主要考查了菱形的判定,以及平行四边形的性质,全等三角形的判定与性质,关键是掌握邻边相等的平行四边形是菱形.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-2)×3=6 | B. | $\sqrt{9}$=±3 | C. | $\root{3}{-8}$=-2 | D. | $\sqrt{25}$-$\sqrt{16}$=$\sqrt{9}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
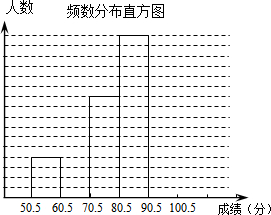 为了让学生了解党的十八大精神,某中学举行了一次“社会主义核心价值观暨八礼四仪知识竞赛”,共有1000名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频数分布表和频数分布直方图,解答下列问题:
为了让学生了解党的十八大精神,某中学举行了一次“社会主义核心价值观暨八礼四仪知识竞赛”,共有1000名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频数分布表和频数分布直方图,解答下列问题:| 频数分布表 | ||
| 分组 | 频数 | 频率 |
| 50.5~60.5 | 4 | 0.08 |
| 60.5~70.5 | 8 | 0.16 |
| 70.5~80.5 | a | 0.20 |
| 80.5~90.5 | 16 | 0.32 |
| 90.5~100.5 | 12 | b |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 13.22×106 | B. | 1.322×107 | C. | 1.322×103 | D. | 0.1322×108 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,P是⊙O外一点,A、B、C是⊙O上的三点,∠AOB=60°,PA、PB分别交$\widehat{ACB}$于M、N两点,则∠APB的范围是0°<∠APB<30°.
如图,P是⊙O外一点,A、B、C是⊙O上的三点,∠AOB=60°,PA、PB分别交$\widehat{ACB}$于M、N两点,则∠APB的范围是0°<∠APB<30°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com