
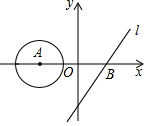
 如图,平面直角坐标系中,⊙A的圆心在x轴上,坐标为(a,0),半径为1,直线l为y=2x-2,若⊙A沿x轴向右运动,当⊙A与直线l有公共点时,点A横坐标a的取值范围是1-$\frac{\sqrt{5}}{2}$≤a≤+$\frac{\sqrt{5}}{2}$.
如图,平面直角坐标系中,⊙A的圆心在x轴上,坐标为(a,0),半径为1,直线l为y=2x-2,若⊙A沿x轴向右运动,当⊙A与直线l有公共点时,点A横坐标a的取值范围是1-$\frac{\sqrt{5}}{2}$≤a≤+$\frac{\sqrt{5}}{2}$. 分析 根据⊙A与L有公共点从左相切开始,到相交,到右相切,所以A移动的距离是左相切到右相切时的距离.
解答 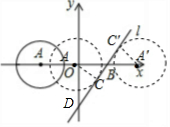 解:如图:当⊙A在直线L的左侧,⊙A与直线L相切时,△BOD∽△ABC,
解:如图:当⊙A在直线L的左侧,⊙A与直线L相切时,△BOD∽△ABC,
∵直线l为y=2x-2,
∴B(1,0),D(0,-2),
∴OB=1,OD=2,
∴$\frac{BC}{OB}=\frac{AC}{AD}$,即$\frac{BC}{1}=\frac{1}{2}$,
∴BC=$\frac{1}{2}$,
∴AB=$\frac{\sqrt{5}}{2}$,
当⊙A在直线L的右侧,⊙A与直线L相切时,同理A′B=$\frac{\sqrt{5}}{2}$,
∴A横坐标a的取值范围是1-$\frac{\sqrt{5}}{2}$≤a≤+$\frac{\sqrt{5}}{2}$,
故答案为:1-$\frac{\sqrt{5}}{2}$≤a≤+$\frac{\sqrt{5}}{2}$.
点评 此题主要考查了坐标与图形的性质和直线与圆的位置关系,关键是知道点A移动距离.


 每课必练系列答案
每课必练系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com