
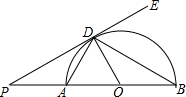
 如图,AB是半圆的直径,O为圆心,AD、AB是半圆的弦,点D是⊙O的切点.
如图,AB是半圆的直径,O为圆心,AD、AB是半圆的弦,点D是⊙O的切点.分析 (1)由AB是半圆的直径,点D是⊙O的切点,得到∠PDA=∠BDO根据AD=BO,推出△AOD是正三角形,得出△PAD≌△BOD,证得PA=DA,即可求得结果.
(2)由tan∠DPB=1,得到∠DPO=∠DOP=45°,由于DM⊥PB,得到$DM=PM=\sqrt{2}$,OP=2$\sqrt{2}$,DO=2,由∠DOB=135°就可以解出弧BD的长度.
解答 (1)解:∵AB是半圆的直径,点D是⊙O的切点,
∴∠PDA=∠BDO
∵AD=BO,
∴△AOD是正三角形,
∴AD=OD,∠PAD=∠BOD,∠APD=30°,
在△PAD与△BOD中,
$\left\{\begin{array}{l}{∠PDA=∠B}\\{AD=OB}\\{∠PAD=∠DOB}\end{array}\right.$,
∴△PAD≌△BOD,
∴PA=DA,
∵PA=2,∠APD=30°,
∴S△PAD=S△BOD=$\sqrt{3}$,∴S△BOD=$\sqrt{3}$;
(2)解:∵点D是⊙O的切点,tan∠DPB=1,
∴∠DPO=∠DOP=45°,
∵DM⊥PB,
∴$DM=PM=\sqrt{2}$,OP=2$\sqrt{2}$,
∴DO=2,
∵∠DOB=135°,
∴由弧长计算公式得:$l=\frac{nπr}{180}=\frac{135π}{180}×2=\frac{3}{2}π$,
∴弧BD的长度是$\frac{3}{2}π$.
点评 本题考查了切线的性质,圆周角定理,三角形的面积,弧长的计算,锐角三角函数,熟记公式是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 第一次右拐60°,第二次左拐120° | B. | 第一次左拐70°,第二次右拐70° | ||
| C. | 第一次左拐65°,第二次左拐115° | D. | 第一次右拐50°,第二次右拐50° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com