
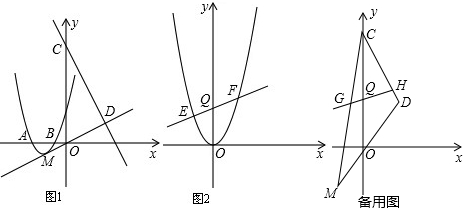
分析 (1)将A(-3,0),B(-1,0)代入y=ax2+bx+3,利用待定系数法即可求出函数的解析式;
(2)先求出抛物线的顶点M的坐标为(-2,-1),则直线OD的解析式为y=$\frac{1}{2}$x.于是设平移的抛物线的顶点坐标为(h,$\frac{1}{2}$h),那么平移的抛物线解析式为y=(x-h)2+$\frac{1}{2}$h.再分两种情况进行讨论:①抛物线经过点C;②抛物线与直线CD只有一个公共点;
(3)①将抛物线平移,当顶点至原点时,其解析式为y=x2,设EF的解析式为y=kx+3(k≠0).假设存在满足题设条件的点P(0,t),过P作GH∥x轴,分别过E,F作GH的垂线,垂足为G,H.由△PEF的内心在y轴上,得出∠GEP=∠EPQ=∠QPF=∠HFP,那么△GEP∽△HFP,根据相似三角形对应边成比例以及根与系数的关系即可求解;
②连结OG.由C(0,9),Q(0,3),可得CQ=2OQ,由M(-2,-1),D(2,1),可得MO=OD.设S△GQO=S,则S△CGQ=2S,S△CGO=3S.为简便起见,不妨设CG=1,MG=x,则S△MGO=3xS.求出S△CGH=(2k+2)S,S四边形MDHG=(6x+6)S-(2k+2)S=(6x-2k+4)S,$\frac{{{S_{四边形MDHG}}}}{{{S_{△CGH}}}}$=$\frac{(6x-2k+4)S}{(2k+2)S}$=$\frac{3x-k+2}{k+1}$①.过点Q作QK∥MD交CD于点K,过点G作GN∥MD交CD于点N,则QK∥GN.再求出k=$\frac{x+1}{2-x}$,代入①式即可求解.
解答 解:(1)∵抛物线y=ax2+bx+3经过A(-3,0),B(-1,0)两点,
∴$\left\{\begin{array}{l}{9a-3b+3=0}\\{a-b+3=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=1}\\{b=4}\end{array}\right.$,
∴抛物线的解析式为y=x2+4x+3;
(2)由(1)配方得y=(x+2)2-1,
∴抛物线的顶点M(-2,-1),
∴直线OD的解析式为y=$\frac{1}{2}$x.于是设平移的抛物线的顶点坐标为(h,$\frac{1}{2}$h),
∴平移的抛物线解析式为y=(x-h)2+$\frac{1}{2}$h.
①当抛物线经过点C时,
∵C(0,9),
∴h2+$\frac{1}{2}$h=9,
解得h=$\frac{-1±\sqrt{145}}{4}$,
∴当 $\frac{-1-\sqrt{145}}{4}$≤h<$\frac{-1+\sqrt{145}}{4}$时,平移的抛物线与射线CD只有一个公共点;
②当抛物线与直线CD只有一个公共点时,将y=(x-h)2+$\frac{1}{2}$h代入y=-4x+9,
得 x2+(-2h+4)x+h2+$\frac{1}{2}$h-9=0,
则△=(-2h+4)2-4(h2+$\frac{1}{2}$h-9)=0,
解得h=$\frac{26}{9}$.
此时抛物线y=(x-$\frac{26}{9}$)2+$\frac{13}{9}$与射线CD唯一的公共点($\frac{8}{9}$,$\frac{49}{9}$),符合题意.
综上:平移的抛物线与射线CD只有一个公共点时,顶点横坐标的值或取值范围是 h=$\frac{26}{9}$或 $\frac{-1-\sqrt{145}}{4}$≤h<$\frac{-1+\sqrt{145}}{4}$;
(3)①将抛物线平移,当顶点至原点时,其解析式为y=x2,设EF的解析式为y=kx+3(k≠0).
假设存在满足题设条件的点P(0,t),
如图,过P作GH∥x轴,分别过E,F作GH的垂线,垂足为G,H.
∵△PEF的内心在y轴上,
∴∠GEP=∠EPQ=∠QPF=∠HFP,
∴△GEP∽△HFP,
∴GP:PH=GE:HF,
∴-xE:xF=(yE-t):(yF-t)=(kxE+3-t):(kxF+3-t),
∴2kxE•xF=(t-3)(xE+xF),
由y=x2,y=-kx+3,得x2-kx-3=0,
∴xE+xF=k,xE•xF=-3,
∴2k(-3)=(t-3)k,
∵k≠0,∴t=-3,
∴y轴的负半轴上存在点P(0,-3),使△PEF的内心在y轴上;
②如图,连结OG.
∵C(0,9),Q(0,3),
∴CQ=2OQ,
又∵M(-2,-1),D(2,1),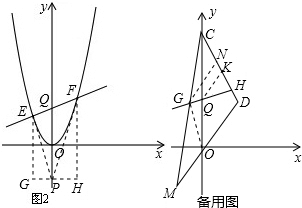 ∴MO=OD.
∴MO=OD.
设S△GQO=S,
∴S△CGQ=2S,S△CGO=3S.
为简便起见,不妨设CG=1,MG=x,则S△MGO=3xS.
∴S△CMO=S△CGO+S△MGO=3S+3xS=(3x+3)S,
∴S△CMD=2S△CMO=(6x+6)S.
设QH=k•QG,由S△CGQ=2S,得S△CQH=2kS,
∴S△CGH=(2k+2)S.
∴S四边形MDHG=(6x+6)S-(2k+2)S=(6x-2k+4)S,
∴$\frac{{{S_{四边形MDHG}}}}{{{S_{△CGH}}}}$=$\frac{(6x-2k+4)S}{(2k+2)S}$=$\frac{3x-k+2}{k+1}$①.
过点Q作QK∥MD交CD于点K,过点G作GN∥MD交CD于点N,则QK∥GN.
∵GK∥MD,∴$\frac{QK}{OD}=\frac{QC}{CO}=\frac{2}{3}$,∴QK=$\frac{2}{3}$OD=$\frac{1}{3}$MD;
∵GN∥MD,∴$\frac{GN}{MD}=\frac{CG}{CM}=\frac{1}{x+1}$,∴$\frac{QK}{GN}=\frac{{\frac{1}{3}MD}}{{\frac{MD}{x+1}}}$=$\frac{x+1}{3}$,∴$\frac{GK}{GN-GK}=\frac{x+1}{3-(x+1)}$=$\frac{x+1}{2-x}$.
∵GK∥GN,∴$\frac{QH}{GH}=\frac{QK}{GN}$,∴$\frac{QH}{QG}=\frac{QK}{GN-QK}=\frac{x+1}{2-x}$,∴k=$\frac{x+1}{2-x}$,
代入①式得:$\frac{{{S_{四边形MDHG}}}}{{{S_{△CGH}}}}$=$\frac{3x-k+2}{k+1}=\frac{{3x-\frac{x+1}{2-x}+2}}{{\frac{x+1}{2-x}+1}}$=-x2+x+1=-(x-$\frac{1}{2}$)2+$\frac{5}{4}$,
∴当x=$\frac{1}{2}$时,$\frac{{{S_{四边形MDHG}}}}{{{S_{△CGH}}}}$有最大值,最大值为$\frac{5}{4}$.
点评 本题是二次函数综合题,其中涉及到利用待定系数法求抛物线的解析式,二次函数平移的规律,一次函数与二次函数的交点,三角形的内心,相似三角形的判定与性质,三角形的面积求法等知识.综合性较强,有一定难度.利用分类讨论、数形结合与方程思想是解题的关键.


科目:初中数学 来源: 题型:解答题
 如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,点P从点A出发,以1cm/s的速度向点D运动;点Q从点C同时出发,以3cm/s的速度向点B运动.规定其中一个动点到达端点时,另一个动点也随之停止运动,设运动时间为t(s).
如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,点P从点A出发,以1cm/s的速度向点D运动;点Q从点C同时出发,以3cm/s的速度向点B运动.规定其中一个动点到达端点时,另一个动点也随之停止运动,设运动时间为t(s).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
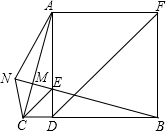 如图,已知正方形ADBF,点E在AD上,且∠AEB=105°,EC∥DF交BD的延长线于C,N为BE延长线上一点,BN交AC于M,且CE=2MN,连结AN、CN,下列结论:
如图,已知正方形ADBF,点E在AD上,且∠AEB=105°,EC∥DF交BD的延长线于C,N为BE延长线上一点,BN交AC于M,且CE=2MN,连结AN、CN,下列结论:| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
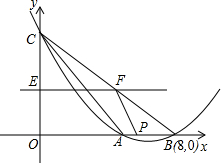 如图,抛物线y=ax2+bx+c(a>0)交x轴于A、B两点,交y轴于C点,A点在B点的左侧,已知B点坐标是(8,0),tan∠ABC=$\frac{1}{2}$,△ABC的面积为8.
如图,抛物线y=ax2+bx+c(a>0)交x轴于A、B两点,交y轴于C点,A点在B点的左侧,已知B点坐标是(8,0),tan∠ABC=$\frac{1}{2}$,△ABC的面积为8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
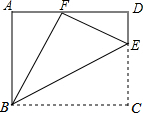 如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD上.若sin∠DFE=$\frac{1}{3}$,则 tan∠EBC的值为$\frac{\sqrt{2}}{2}$.
如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD上.若sin∠DFE=$\frac{1}{3}$,则 tan∠EBC的值为$\frac{\sqrt{2}}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com