
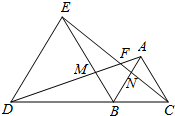
 如图,A,B,C,D,E,F,M,N是某公园里的8个独立的景点,D,E,B三个景点之间的距离相等;A,B,C三个景点距离相等.其中D,B,C在一条直线上,E,F,N,C在同一直线上,D,M,F,A也在同一条直线上.游客甲从E点出发,沿E→F→N→C→A→B→M游览,同时,游客乙从D点出发,沿D→M→F→A→C→B→N游览.若两人的速度相同且在各景点游览的时间相同,甲、乙两人谁最先游览完?请说明理由.
如图,A,B,C,D,E,F,M,N是某公园里的8个独立的景点,D,E,B三个景点之间的距离相等;A,B,C三个景点距离相等.其中D,B,C在一条直线上,E,F,N,C在同一直线上,D,M,F,A也在同一条直线上.游客甲从E点出发,沿E→F→N→C→A→B→M游览,同时,游客乙从D点出发,沿D→M→F→A→C→B→N游览.若两人的速度相同且在各景点游览的时间相同,甲、乙两人谁最先游览完?请说明理由.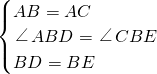 ,
, ,
,

 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
 如图,已知A,B两点是反比例函数y=
如图,已知A,B两点是反比例函数y=| 4 | x |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com