
【题目】如图,在ABCD中,已知AD>AB.
(1)实践与操作:作∠BAD的平分线交BC于点E,在AD上截取AF=AB,连接EF;(要求:尺规作图,保留作图痕迹,不写作法)
(2)猜想并证明:猜想四边形ABEF的形状,并给予证明.
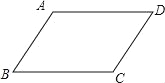
【答案】(1)详见解析;(2)四边形ABEF是菱形,理由详见解析.
【解析】
试题分析:(1)由角平分线的作法容易得出结果,在AD上截取AF=AB,连接EF;画出图形即可;(2)由平行四边形的性质和角平分线得出∠BAE=∠AEB,证出BE=AB,由(1)得:AF=AB,得出BE=AF,即可得出结论.
试题解析:解:(1)如图所示:
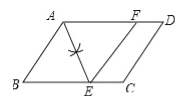
(2)四边形ABEF是菱形;理由如下:
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠AEB,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴BE=AB,
由(1)得:AF=AB,
∴BE=AF,
又∵BE∥AF,
∴四边形ABEF是平行四边形,
∵AF=AB,
∴四边形ABEF是菱形.


科目:初中数学 来源: 题型:
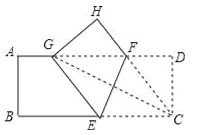
【题目】如图,将矩形纸片ABCD(AD>AB)折叠,使点C刚好落在线段AD上,且折痕分别与边BC,AD相交,设折叠后点C,D的对应点分别为点G,H,折痕分别与边BC,AD相交于点E,F.
(1)判断四边形CEGF的形状,并证明你的结论;
(2)若AB=3,BC=9,求线段CE的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
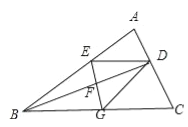
【题目】如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.
(1)请判断四边形EBGD的形状,并说明理由;
(2)若∠ABC=30°,∠C=45°,ED=2![]() ,点H是BD上的一个动点,求HG+HC的最小值.
,点H是BD上的一个动点,求HG+HC的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】被誉为“里下河的明珠”的九龙口自然保护区,地处射阳湖腹部的建湖县九龙口镇,由蚬河等9条自然河道汇集而成,水面约6670万平方米,这里藏垒水禽野味,广植柴蒲菱藕,盛产鱼虾螃蟹,有“金滩银荡”之美誉,是天然的“聚宝盆”,其中6670万平方米用科学记数法表示为平方米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一个我们喜欢玩的魔方,它是由若干个小正方体组成的一个大正方体,在这个大正方体的六个面上,分别涂有6种不同的颜色.根据你的观察与想象回答下列问题:①有几个小正方体只有一个面被涂有颜色?②有几个小正方体有两个面被涂有颜色?③有几个小正方体有三个面被涂有颜色?
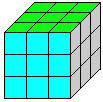
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店有2个进价不同的计算器都卖了80元,其中一个盈利60%,另一个亏本20%,在这笔买卖中,这家商店( )
A.赚了10元
B.赔了10元
C.不赔不赚
D.赚了8元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF.
(1)观察猜想
如图1,当点D在线段BC上时,
①BC与CF的位置关系为: .
②BC,CD,CF之间的数量关系为: ;(将结论直接写在横线上)
(2)数学思考
如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)拓展延伸
如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE.若已知AB=2![]() ,CD=
,CD=![]() BC,请求出GE的长.
BC,请求出GE的长.
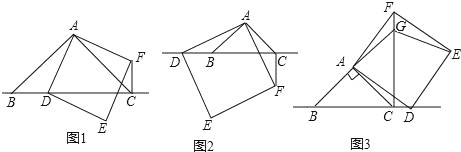
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com