
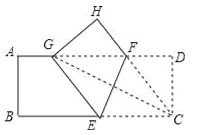
【题目】如图,将矩形纸片ABCD(AD>AB)折叠,使点C刚好落在线段AD上,且折痕分别与边BC,AD相交,设折叠后点C,D的对应点分别为点G,H,折痕分别与边BC,AD相交于点E,F.
(1)判断四边形CEGF的形状,并证明你的结论;
(2)若AB=3,BC=9,求线段CE的取值范围.
【答案】(1)四边形CEGF为菱形,理由详见解析;(2)3≤CE≤5.
【解析】
试题分析:(1)根据折叠的性质,易证△EFG是等腰三角形,根据等腰三角形的性质可得GF=EC,又由GF∥EC,即可得四边形CEGF为平行四边形,根据邻边相等的平行四边形是菱形,即可得四边形BGEF为菱形;(2)如图1,当G与A重合时,CE取最大值,由折叠的性质得CD=DG,∠CDE=∠GDE=45°,推出四边形CEGD是矩形,根据矩形的性质即可得到CE=CD=AB=3;如图2,当F与D重合时,CE取最小值,由折叠的性质得AE=CE,根据勾股定理即可得到结论.
试题解析:(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠GFE=∠FEC,
∵图形翻折后点G与点C重合,EF为折线,
∴∠GEF=∠FEC,
∴∠GFE=∠FEG,
∴GF=GE,
∵图形翻折后BC与GE完全重合,
∴BE=EC,
∴GF=EC,
∴四边形CEGF为平行四边形,
∴四边形CEGF为菱形;
(2)解:如图1,当F与D重合时,CE取最小值,
由折叠的性质得CD=DG,∠CDE=∠GDE=45°,
∵∠ECD=90°,
∴∠DEC=45°=∠CDE,
∴CE=CD=DG,
∵DG∥CE,
∴四边形CEGD是矩形,
∴CE=CD=AB=3;
如图2,当G与A重合时,CE取最大值,
由折叠的性质得AE=CE,
∵∠B=90°,
∴AE2=AB2+BE2,即CE2=32+(9﹣CE)2,
∴CE=5,
∴线段CE的取值范围3≤CE≤5.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图1,在△OMN中,∠MON=90°,OM=6cm,∠OMN=30°.等边△ABC的顶点B与点O重合,BC在OM上,点A恰好在MN上.
(1)求等边△ABC的边长;
(2)如图2,将等边△ABC沿OM方向以1cm/s的速度平移,边AB、AC分别与MN交于点E、F,在△ABC平移的同时,点P从△ABC的顶点B出发,以2cm/s的速度沿折线B→A→C运动,当点P达到点C时,点P停止运动,△ABC也随之停止平移.设△ABC平移时间为t(s)
①用含t的代数式表示AE的长,并写出t的取值范围;
②在点P沿折线B→A→C运动的过程中,是否在某一时刻,点P、E、F组成的三角形为等腰三角形?若存在,求出此时t值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张长方形的纸对折,可得到一条折痕(图中虚线),继续对折,对折时每次折痕与上次的折痕保持平行,连续对折3次后,可以得到7条折痕,那么对折4次可以得到多少条折痕?如果对折n次呢?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】服装店销售某款服装,一件服装的标价为300元,若按标价的八折销售,仍可获利60元,则这款服装每件的标价比进价多
A. 60元 B. 80元 C. 120元 D. 180元
查看答案和解析>>
科目:初中数学 来源: 题型:
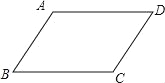
【题目】如图,在ABCD中,已知AD>AB.
(1)实践与操作:作∠BAD的平分线交BC于点E,在AD上截取AF=AB,连接EF;(要求:尺规作图,保留作图痕迹,不写作法)
(2)猜想并证明:猜想四边形ABEF的形状,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对三角形的高、中线和角平分线概念理解错误的是( )
A.直角三角形只有一条高
B.钝角三角形有两条高在三角形外部
C.锐角三角形的三条高、三条中线、三条角平分线分别交于一点
D.任意三角形都有三条高、三条中线、三条角平分线
查看答案和解析>>
科目:初中数学 来源: 题型:
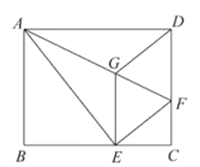
【题目】(2016湖北襄阳第24题)
如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.
(1)求证:四边形EFDG是菱形;
(2)探究线段EG,GF,AF之间的数量关系,并说明理由;
(3)若AG=6,EG=2![]() ,求的长.
,求的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com