
【题目】(2016湖北襄阳第24题)
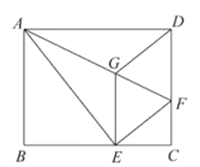
如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.
(1)求证:四边形EFDG是菱形;
(2)探究线段EG,GF,AF之间的数量关系,并说明理由;
(3)若AG=6,EG=2![]() ,求的长.
,求的长.
科目:初中数学 来源: 题型:
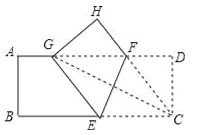
【题目】如图,将矩形纸片ABCD(AD>AB)折叠,使点C刚好落在线段AD上,且折痕分别与边BC,AD相交,设折叠后点C,D的对应点分别为点G,H,折痕分别与边BC,AD相交于点E,F.
(1)判断四边形CEGF的形状,并证明你的结论;
(2)若AB=3,BC=9,求线段CE的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店有2个进价不同的计算器都卖了80元,其中一个盈利60%,另一个亏本20%,在这笔买卖中,这家商店( )
A.赚了10元
B.赔了10元
C.不赔不赚
D.赚了8元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是按规律排列的一列式子:
第1个式子:1-![]()
第2个式子:2-![]()

![]() ;
;
第3个式子:3—![]()
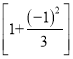
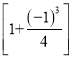
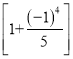
 .
.
(1)分别计算这三个式子的结果(直接写答案);
(2)写出第2017个式子的形式(中间部分用省略号,两端部分必须写详细),然后推测出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中共装有红球、黄球和蓝球320个,这些球除颜色外都相同.小明每次从中任意摸出一个球,记下颜色后将球放回并搅匀,通过多次重复试验,算得摸到红球的频率是25 %,则估计这只袋子中有红球________.
查看答案和解析>>
科目:初中数学 来源: 题型:
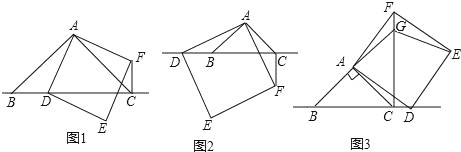
【题目】△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF.
(1)观察猜想
如图1,当点D在线段BC上时,
①BC与CF的位置关系为: .
②BC,CD,CF之间的数量关系为: ;(将结论直接写在横线上)
(2)数学思考
如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)拓展延伸
如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE.若已知AB=2![]() ,CD=
,CD=![]() BC,请求出GE的长.
BC,请求出GE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com