练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知关于x的一元二次方程x2+ax﹣（m﹣1）（m+2）=0，对于任意实数a都有实数根，则m的取值范围是 ．

    【答案】m≤﹣2或m≥1
    【解析】解：∵关于x的一元二次方程x2+ax﹣（m﹣1）（m+2）=0，对于任意实数a都有实数根， ∴△=a2+4（m﹣1）（m+2）≥0，
    ∴只要4（m﹣1）（m+2）≥0，方程一定有实数根，
    解得：m≤﹣2或m≥1．
    所以答案是m≤﹣2或m≥1．
    【考点精析】认真审题，首先需要了解求根公式(根的判别式△=b2-4ac，这里可以分为3种情况：1、当△>0时，一元二次方程有2个不相等的实数根2、当△=0时，一元二次方程有2个相同的实数根3、当△<0时，一元二次方程没有实数根)．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】(2016湖北襄阳第24题)

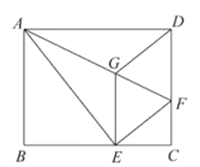
    如图，将矩形ABCD沿AF折叠，使点D落在BC边的点E处，过点E作EG∥CD交AF于点G，连接DG．

    (1)求证：四边形EFDG是菱形；

    (2)探究线段EG，GF，AF之间的数量关系，并说明理由；

    (3)若AG=6，EG=2，求的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

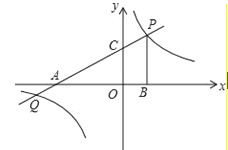
    【题目】如图，直线y= x+b，分别交x轴，y轴于点A、C，点P是直线AC与双曲线y=在第一象限内的交点，过点P作PB⊥x轴于点B，若OB=2，PB=3.

    （1）填空：k=　 　；

    （2）求△ABC的面积；

    （3）求在第一象限内，当x取何值时，一次函数的值小于反比例函数的值？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】(10分)如图，在△ABC中，AB=AC，AB的垂直平分线交AB于M，交AC于N．

    （1）若∠ABC=70°，则∠MNA的度数是　　．

    （2）连接NB，若AB=8cm，△NBC的周长是14cm．

    ①求BC的长；

    ②在直线MN上是否存在P，使由P、B、C构成的△PBC的周长值最小？若存在，标出点P的位置并求△PBC的周长最小值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“抛掷1枚均匀硬币正面朝上”是（ ）

    A.必然事件B.不可能事件C.随机事件D.不能确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列运算中，正确的是（ ）
    A.4x-x=2x
    B.2x·x4=x5
    C.x2y÷y=x2
    D.(-3x)3=-9x3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

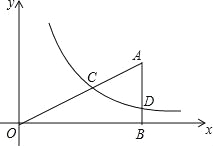
    【题目】(2016宁夏第24题)如图，Rt△ABO的顶点O在坐标原点，点B在x轴上，∠ABO=90°，∠AOB=30°，OB=2，反比例函数y=（x＞0）的图象经过OA的中点C，交AB于点D．

    （1）求反比例函数的关系式；

    （2）连接CD，求四边形CDBO的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若代数式2x2﹣4x﹣5的值为7，则x2﹣2x﹣2的值为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

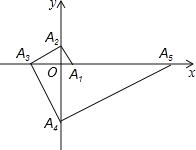
    【题目】如图，点A1的坐标为（1，0），A2在y轴的正半轴上，且∠A1A2O=30°，过点A2作A2A3⊥A1A2，垂足为A2，交x轴于点A3；过点A3作A3A4⊥A2A3，垂足为A3，交y轴于点A4；过点A4作A4A5⊥A3A4，垂足为A4，交x轴于点A5；过点A5作A5A6⊥A4A5，垂足为A5，交y轴于点A6；…按此规律进行下去，则点A2016的纵坐标为 ．

    查看答案和解析>>

    同步练习册答案