
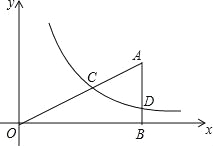
【题目】(2016宁夏第24题)如图,Rt△ABO的顶点O在坐标原点,点B在x轴上,∠ABO=90°,∠AOB=30°,OB=2![]() ,反比例函数y=
,反比例函数y=![]() (x>0)的图象经过OA的中点C,交AB于点D.
(x>0)的图象经过OA的中点C,交AB于点D.
(1)求反比例函数的关系式;
(2)连接CD,求四边形CDBO的面积.
【答案】(1)、y=![]() ;(2)、
;(2)、![]()
【解析】
试题分析:(1)、解直角三角形求得AB,作CE⊥OB于E,根据平行线分线段成比例定理和三角形中位线的性质求得C的坐标,然后根据待定系数法即可求得反比例函数的解析式;(2)、求得D的坐标,进而求得AD的长,得出△ACD的面积,然后根据S四边形CDBO=S△AOB﹣S△ACD即可求得.
试题解析:(1)、∵∠ABO=90°,∠AOB=30°,OB=2![]() , ∴AB=
, ∴AB=![]() OB=2, 作CE⊥OB于E,
OB=2, 作CE⊥OB于E,
∵∠ABO=90°, ∴CE∥AB, ∴OC=AC, ∴OE=BE=![]() OB=
OB=![]() ,CE=
,CE=![]() AB=1, ∴C(
AB=1, ∴C(![]() ,1),
,1),
∵反比例函数y=![]() (x>0)的图象经过OA的中点C, ∴1=
(x>0)的图象经过OA的中点C, ∴1=![]() , ∴k=
, ∴k=![]() ,
,
∴反比例函数的关系式为y=![]() ;
;
(2)、∵OB=2![]() , ∴D的横坐标为2
, ∴D的横坐标为2![]() , 代入y=
, 代入y=![]() 得,y=
得,y=![]() , ∴D(2
, ∴D(2![]() ,
,![]() ), ∴BD=
), ∴BD=![]() ,
,
∵AB=2, ∴AD=![]() , ∴S△ACD=
, ∴S△ACD=![]() ADBE=
ADBE=![]() ×
×![]() ×
×![]() =
=![]() ,
,
∴S四边形CDBO=S△AOB﹣S△ACD=![]() OBAB﹣
OBAB﹣![]() =
=![]() ×2
×2![]() ×2﹣
×2﹣![]() =
=![]() .
.



科目:初中数学 来源: 题型:
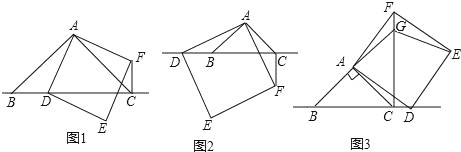
【题目】△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF.
(1)观察猜想
如图1,当点D在线段BC上时,
①BC与CF的位置关系为: .
②BC,CD,CF之间的数量关系为: ;(将结论直接写在横线上)
(2)数学思考
如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)拓展延伸
如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE.若已知AB=2![]() ,CD=
,CD=![]() BC,请求出GE的长.
BC,请求出GE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
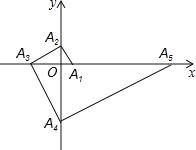
【题目】如图,点A1的坐标为(1,0),A2在y轴的正半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2,垂足为A2,交x轴于点A3;过点A3作A3A4⊥A2A3,垂足为A3,交y轴于点A4;过点A4作A4A5⊥A3A4,垂足为A4,交x轴于点A5;过点A5作A5A6⊥A4A5,垂足为A5,交y轴于点A6;…按此规律进行下去,则点A2016的纵坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个学生从点A向北偏东60方向走40米,到达点B,再从B沿北偏西30方向走 30米,到达点C,此时,恰好在点A的正北方向,则下列说法正确的是( )
A. 点A到BC的距离为30米 B. 点B在点C的南偏东30方向40米处
C. 点A在点B的南偏西60方向30米处 D. 以上都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P(x0,y0)和直线y=kx+b,则点P到直线y=kx+b的距离证明可用公式d=![]() 计算.
计算.
例如:求点P(﹣1,2)到直线y=3x+7的距离.
解:因为直线y=3x+7,其中k=3,b=7.
所以点P(﹣1,2)到直线y=3x+7的距离为:d=![]() =
=![]() =
=![]() =
=![]() .
.
根据以上材料,解答下列问题:
(1)求点P(1,﹣1)到直线y=x﹣1的距离;
(2)已知⊙Q的圆心Q坐标为(0,5),半径r为2,判断⊙Q与直线y=![]() x+9的位置关系并说明理由;
x+9的位置关系并说明理由;
(3)已知直线y=﹣2x+4与y=﹣2x﹣6平行,求这两条直线之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为提倡节约用水,采取分段收费.若每户每月用水不超过20m3 , 每立方米收费2元;若用水超过20m3 , 超过部分每立方米加收1元.小明家5月份交水费64元,则他家该月用水( )m3 .
A.38
B.34
C.28
D.44
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°
(1)先作∠ACB的平分线交AB边于点P,再以点P为圆心,PA长为半径作⊙P;(要求:尺规作图,保留作图痕迹,不写作法)
(2)请你判断(1)中BC与⊙P的位置关系,并证明你的结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com