
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:①△ABG≌△AFG;②∠EAG=45°;③BG=GC;④AG∥CF.其中正确结论的个数是( )
A.4
B.3
C.2
D.1
【答案】A
【解析】解:∵四边形ABCD是正方形,
∴AB=AD=DC=6,∠B=D=90°,
∵CD=3DE,
∴DE=2,
∵△ADE沿AE折叠得到△AFE,
∴DE=EF=2,AD=AF,∠D=∠AFE=∠AFG=90°,
∴AF=AB,
∵在Rt△ABG和Rt△AFG中![]() ,
,
∴Rt△ABG≌Rt△AFG(HL),∴①正确;
∵Rt△ABG≌Rt△AFG,
∴BG=FG,∠AGB=∠AGF,
设BG=x,则CG=BC﹣BG=6﹣x,GE=GF+EF=BG+DE=x+2,
在Rt△ECG中,由勾股定理得:CG2+CE2=EG2 ,
∵CG=6﹣x,CE=4,EG=x+2
∴(6﹣x)2+42=(x+2)2
解得:x=3,
∴BG=GF=CG=3,∴③正确;
∵CG=GF,
∴∠CFG=∠FCG,
∵∠BGF=∠CFG+∠FCG,
又∵∠BGF=∠AGB+∠AGF,
∴∠CFG+∠FCG=∠AGB+∠AGF,
∵∠AGB=∠AGF,∠CFG=∠FCG,
∴∠AGB=∠FCG
∴AG∥CF,∴④正确;
∵△ADE沿AE折叠得到△AFE,
∴△DAE≌△FAE,
∴∠DAE=∠FAE,
∵△ABG≌△AFG,
∴∠BAG=∠FAG,
∵∠BAD=90°,
∴∠EAG=∠EAF+∠GAF= ![]() ×90°=45°,∴②正确;
×90°=45°,∴②正确;
故选A.
【考点精析】利用正方形的性质和翻折变换(折叠问题)对题目进行判断即可得到答案,需要熟知正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.


科目:初中数学 来源: 题型:
【题目】纳米是非常小的长度单位,1纳米=10﹣9米.某种病菌的长度约为50纳米,用科学记数法表示该病菌的长度,结果正确的是( )
A.5×10﹣10米B.5×10﹣9米C.5×10﹣8米D.5×10﹣7米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杨辉三角是一个由数字排列成昀三角形数表,一般形式如图所示,其中每一横行都表示![]() (此处
(此处![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() )的展开式中的系数,杨辉三角最本质的特征是,它的两条斜边都是由数字
)的展开式中的系数,杨辉三角最本质的特征是,它的两条斜边都是由数字![]() 组成的,而其余的数则是等于它“肩”上的两个数之和.
组成的,而其余的数则是等于它“肩”上的两个数之和.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
上图的构成规律你看懂了吗?
请你直接写出(a+b)7 =______.
杨辉三角还有另一个特征
(1)从第二行到第五行,每一行数字组成的数(如第三行为![]() )都是上一行的数与______积.
)都是上一行的数与______积.
(2)由此你可写出![]() =______.
=______.
(3)由第_____行可写出![]() =______.
=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
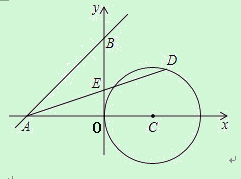
【题目】如图,已知直线y=x+4与两坐标轴分别交于A、B两点,⊙C的圆心坐标为 (2,O),半径为2,若D是⊙C上的一个动点,线段DA与y轴交于点E,则△ABE面积的最小值和最大值分别是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种细胞的直径是0.00000095米,将0.00000095米用科学记数法表示为( )
A.9.5×10﹣7
B.9.5×10﹣8
C.0.95×10﹣7
D.95×10﹣8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com