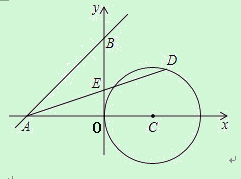
【题目】如图，已知直线y=x+4与两坐标轴分别交于A、B两点，⊙C的圆心坐标为 （2，O），半径为2，若D是⊙C上的一个动点，线段DA与y轴交于点E，则△ABE面积的最小值和最大值分别是　 　．

参考答案：

【答案】8﹣2和8+2

【解析】首先由一次函数解析式求出OA、OB的长，而△ABE中，BE边上的高是OA，且OA为定值，所以求△ABE面积的最小值和最大值，转化为求BE的最小值和最大值。过点A作⊙C的两条切线AD、AD′，当动点运动到D点时，BE最小，即△ABE面积最小；当动点运动到D′点时，BE最大，即△ABE面积最大。最后根据比例求出BE 、BE′的值，进而求出△ABE面积的最小值和最大值．

解：由y=x+4得：

当x=0时，y=4，当y=0时，x=﹣4，

∴OA=4，OB=4，

∵△ABE的边BE上的高是OA，

∴△ABE的边BE上的高是4，

∴要使△ABE的面积最大或最小，只要BE取最大值或最小值即可，

过A作⊙C的两条切线，如图，

当动点运动到D点时，BE最小，即△ABE面积最小；

当动点运动到D′点时，BE最大，即△ABE面积最大；

∵x轴⊥y轴，OC为半径，

∴EE′是⊙C切线，

∵AD′是⊙C切线，

∴OE′=E′D′，

设E′O=E′D′=x，

∵AC=4+2=6，CD′=2，AD′是切线，

∴∠AD′C=90°，由勾股定理得：AD′=4，

∴sin∠CAD′==，

∴=，

解得：x=，

∴BE′=4+，BE=4﹣，

∴△ABE的最小值是×（4﹣）×4=8﹣2，

最大值是：×（4+）×4=8+2，

故答案为：8﹣2和8+2．

关闭