
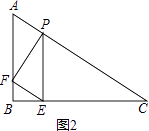
【题目】已知Rt△ABC中,∠B=90°,AC=20,AB=10,P是边AC上一点(不包括端点A、C),过点P作PE⊥BC于点E,过点E作EF∥AC,交AB于点F.设PC=x,
PE=y.
(1)求y与x的函数关系式;
(2)是否存在点P使△PEF是Rt△?若存在,求此时的x的值;若不存在,请说明理由.
【答案】
(1)解:在Rt△ABC中,∠B=90°,AC=20,AB=10,
∴sinC= ![]() ,
,
∵PE⊥BC于点E,
∴sinC= ![]() =
= ![]() ,
,
∵PC=x,PE=y,
∴y= ![]() x(0<x<20)
x(0<x<20)
(2)解:存在点P使△PEF是Rt△,
①如图1,当∠FPE=90°时,四边形PEBF是矩形,BF=PE= ![]() x,
x,
四边形APEF是平行四边形,PE=AF= ![]() x,
x,
∵BF+AF=AB=10,
∴x=10;
②如图2,当∠PFE=90°时,Rt△APF∽Rt△ABC,
∠ARP=∠C=30°,AF=40﹣2x,
平行四边形AFEP中,AF=PE,即:40﹣2x= ![]() x,
x,
解得x=16;
③当∠PEF=90°时,此时不存在符合条件的Rt△PEF.
综上所述,当x=10或x=16,存在点P使△PEF是Rt△.

【解析】考查了相似三角形的判定与性质,平行四边形的性质,矩形的性质,解直角三角形,注意分类思想的运用,综合性较强,难度中等.(1)在Rt△ABC中,根据三角函数可求y与x的函数关系式;(2)分三种情况:①如图1,当∠FPE=90°时,②如图2,当∠PFE=90°时,③当∠PEF=90°时,进行讨论可求x的值.
【考点精析】通过灵活运用平行四边形的性质和矩形的性质,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;矩形的四个角都是直角,矩形的对角线相等即可以解答此题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,把一个圆锥沿母线OA剪开,展开后得到扇形AOC,已知圆锥的高h为12cm,OA=13cm,则扇形AOC中 ![]() 的长是cm(计算结果保留π).
的长是cm(计算结果保留π).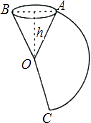
查看答案和解析>>
科目:初中数学 来源: 题型:
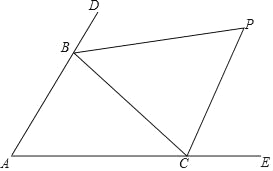
【题目】如图,△ABC中,分别延长△ABC的边AB、AC到D、E,∠CBD与∠BCE的平分线相交于点P,爱动脑筋的小明在写作业的时发现如下规律:
(1)若∠A=60°,则∠P= °;
(2)若∠A=40°,则∠P= °;
(3)若∠A=100°,则∠P= °;
(4)请你用数学表达式归纳∠A与∠P的关系 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD各个顶点的坐标分别为(﹣2,8),(﹣11,6),(﹣14,0),(0,0).
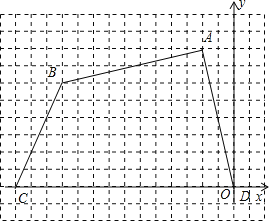
(1)求这个四边形的面积.
(2)如果把原来的四边形ABCD向下平移3个单位长度,再向左平移2个单位长度后得到新的四边形A1B2C3D4,请直接写出平移后的四边形各点的坐标和新四边形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用A、B两种机器人搬运大米,A型机器人比B型机器人每小时多搬运20袋大米,A型机器人搬运700袋大米与B型机器人搬运500袋大米所用时间相等.求A、B型机器人每小时分别搬运多少袋大米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是矩形ABCD的一条对角线. 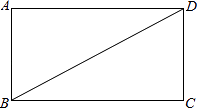
(1)作BD的垂直平分线EF,分别交AD、BC于点E、F,垂足为点O.(要求用尺规作图,保留作图痕迹,不要求写作法);
(2)求证:DE=BF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是矩形ABCD的一条对角线. 
(1)作BD的垂直平分线EF,分别交AD、BC于点E、F,垂足为点O.(要求用尺规作图,保留作图痕迹,不要求写作法);
(2)求证:DE=BF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(背景知识)数轴上有两点 A、B 对应的数为 a、b,AB表示这两个点间的距离,这两个点的中点所对应的数为![]() .
.
已知数轴上有三点 A、B、C,对应的数分别为 a、b、c,a、b、c 满足以下两个条件:①![]() ② a-b+c=0.
② a-b+c=0.
(1)求出 a、b、c 的值;
(2)若数轴上有一点 P,PA=3PB,求出满足条件的P点所对应的数;
(3)点A以每秒钟2个单位长度的速度向左运动,点B以每秒钟4个单位长度的速度向右运动,点C以每秒钟6个单位长度的速度向右运动.它们同时出发,M为AB 的中点,N为BC的中点,Q为AC的中点,O为原点,试求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com