
如图, AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
(1)求证:AD=AE;
(2) 连接OA,BC,试判断直线OA,BC的关系,并说明理由.

(1)证明见解析;(2)互相垂直,理由见解析.
【解析】
试题分析:(1)根据全等三角形的判定方法,证明△ACD≌△ABE,即可得出AD=AE,
(2)根据已知条件得出△ADO≌△AEO,得出∠DAO=∠EAO,即可判断出OA是∠BAC的平分线,即OA⊥BC.
试题解析:(1)证明:在△ACD与△ABE中,
∵∠A=∠A,∠ADC=∠AEB=90°,AB=AC,
∴△ACD≌△ABE,
∴AD=AE.
(2)互相垂直,
在Rt△ADO与△AEO中,
∵OA=OA,AD=AE,
∴△ADO≌△AEO,
∴∠DAO=∠EAO,
即OA是∠BAC的平分线,
又∵AB=AC,
∴OA⊥BC.
考点:全等三角形的判定与性质.


科目:初中数学 来源:2013-2014学年辽宁省丹东市九年级第一次模拟考试数学试卷(解析版) 题型:选择题
一家鞋店在一段时间内销售了某种男鞋200双,各种尺码鞋的销售量如下表所示:
尺码/厘米 | 23 | 23.5 | 24 | 24.5 | 25 | 25.5 | 26 |
销售量/双 | 5 | 10 | 22 | 39 | 56 | 43 | 25 |
一般来讲,鞋店老板比较关心哪种尺码的鞋最畅销,也就是关心卖出的鞋的尺码组成的一组数据的( ) A.平均数 B.中位数 C.众数 D.方差
查看答案和解析>>
科目:初中数学 来源:2013-2014学年福建省厦门市业质量检查数学试卷(解析版) 题型:解答题
袋子中装有2个红球,1个黄球,它们除颜色外其余都相同.小明和小英做摸球游戏,约定一次游戏规则是:小英先从袋中任意摸出1个球记下颜色后放回,小明再从袋中摸出1个球记下颜色后放回,如果两人摸到的球的颜色相同,小英赢,否则小明赢.
(1)请用树状图或列表格法表示一次游戏中所有可能出现的结果;
(2)这个游戏规则对双方公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年福建省厦门市业质量检查数学试卷(解析版) 题型:选择题
在平面直角坐标系中,将线段OA绕原点O逆时针旋转90°,记点A(-1,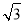 )的对应点为A1,则A1的坐标为( )
)的对应点为A1,则A1的坐标为( )
A.(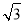 ,1) B.(1,
,1) B.(1,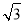 ) C.(-
) C.(-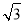 ,-1) D.(-1,-
,-1) D.(-1,-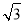 )
)
查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖南省长沙市长郡教育集团九年级期末考试数学试卷(解析版) 题型:解答题
如图甲,四边形OABC的边OA、OC分别在x轴、y轴的正半轴上,顶点在B点的抛物线交x轴于点A、D,交y轴于点E,连结AB、AE、BE.已知tan∠CBE= ,A(3,0),D(-1,0),E(0,3).
,A(3,0),D(-1,0),E(0,3).
(1)求抛物线的解析式及顶点B的坐标;
(2)求证:CB是△ABE外接圆的切线;
(3)试探究坐标轴上是否存在一点P,使以D、E、P为顶点的三角形与△ABE相似,若存在,直接写出点P的坐标;若不存在,请说明理由;
(4)设△AOE沿x轴正方向平移t个单位长度(0<t≤3)时,△AOE与△ABE重叠部分的面积为s,求s与t之间的函数关系式,并指出t的取值范围.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖南省长沙市长郡教育集团九年级期末考试数学试卷(解析版) 题型:填空题
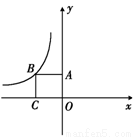
如图,四边形OABC是边长为1的正方形,反比例函数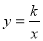 的图象过点B,则
的图象过点B,则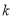 的值为 .
的值为 .
查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖南省长沙市长郡教育集团九年级期末考试数学试卷(解析版) 题型:选择题
到三角形三条边的距离都相等的点是这个三角形的( )
A.三条中线的交点 B.三条高的交点
C.三条边的垂直平分线的交点 D.三条角平分线的交点
查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖北省黄冈市中考模拟考试数学试卷A(解析版) 题型:解答题
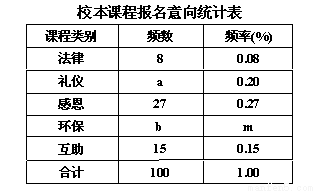
某校有学生2100人,在“文明我先行”的活动中,开设了“法律、礼仪、感恩、环保、互助”五门校本课程,规定每位学生必须且只能选择一门。为了解学生的报名意向学校随机调查了100名学生,并制成如右统计表:
(1)在这次调查活动中,学校采取的调查的方式是 (填写“普查”或“抽样调查”)
(2)a= ,b= ,m= .
(3)如果要画“校本课程报名意向扇形统计图”,那么“礼仪”类校本课程所对应的扇形圆心角的度数是 .
(4)请你统计,全校选择“感恩”类校本课程的学生约有 人.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖北省鄂州市九年级4月调研考试数学试卷(解析版) 题型:解答题
为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担,李明按照相关政策投资销售本市生产的一种新型节能灯,已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=-10x+500.
⑴李明在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?
⑵设李明获得的利润为W(元),当销售单价定为多少元时,每月可获得最大利润?
⑶物价部门规定,这种节能灯的销售单价不得高于25元,如果李明想要每月获得的利润不低于3000元,那么政府为他承担的总差价最少为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com