解:(1)∵a=1>0,
∴抛物线开口向上,
当x=0时,y=0
2+(b-1)×0-5=-5,
∴它与y轴的交点坐标为(0,-5);
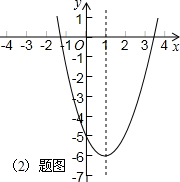
(2)抛物线的对称轴为x=1,
∴-

=-
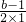
=1,
解得b=-1,
故抛物线的解析式为y=x
2-2x-5;
图象如右;
(3)∵b>3,
∴抛物线的对称轴x=-

=-
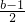
<-1,
∴对称轴在点P的左侧,
∵直线PA⊥y轴,且P(-1,c),BP=2PA,
∴点B的坐标为(-3,c),
把点B(-3,c)、P(-1,c)代入抛物线解析式y=x
2+(b-1)x-5得,
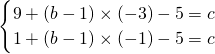
,
解得
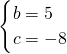
,
∴抛物线所对应的二次函数解析式为y=x
2+4x-5;
[或:∵点B(-3,c)、P(-1,c),
∴BP的中点(-2,c)在抛物线的对称轴上,
∴-

=-
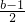
=-2,解得b=5.]
分析:(1)根据a值大于0,判断抛物线的开口向上,令x=0求出函数值y,就是抛物线与y轴的交点坐标;
(2)根据对称轴解析式列式求出b的值,从而得到抛物线解析式,再根据抛物线与坐标轴的交点与顶点坐标作出草图即可;
(3)先根据b>3判断出点P在对称轴的左侧,然后根据BP=2PA求出点B的坐标,然后把点P、B的坐标代入抛物线解析式,利用待定系数法求出b、c的值,即可写出该抛物线对应的二次函数解析式.[或者根据点BP的中点在抛物线的对称轴上,利用对称轴解析式列式进行计算求解b的值.]
点评:本题是对二次函数的综合考查,抛物线的开口方向,与坐标轴的交点的求解,以及待定系数法求二次函数解析式,综合性题目但难度不大,只要仔细分析,认真计算便不难求解.

 已知:抛物线y=x2+(b-1)x-5.
已知:抛物线y=x2+(b-1)x-5.
 =-
=-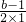 =1,
=1, =-
=-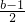 <-1,
<-1,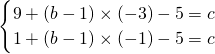 ,
,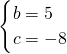 ,
, =-
=-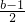 =-2,解得b=5.]
=-2,解得b=5.]

 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案