
如图,抛物线C1:y=(x+m)2(m为常数,m>0),平移抛物线y=﹣x2,使其顶点D在抛物线C1位于y轴右侧的图象上,得到抛物线C2.抛物线C2交x轴于A,B两点(点A在点B的左侧),交y轴于点C,设点D的横坐标为a.
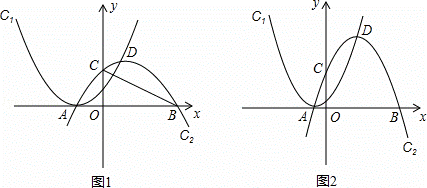
(1)如图1,若m=.
①当OC=2时,求抛物线C2的解析式;
②是否存在a,使得线段BC上有一点P,满足点B与点C到直线O P的距离之和最大且AP=BP?若存在,求出a的值;若不存在,请说明理由;
P的距离之和最大且AP=BP?若存在,求出a的值;若不存在,请说明理由;
(2)如图2,当OB=2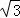 ﹣m(0<m<
﹣m(0<m<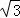 )时,请直接写出到△ABD的三边所在直线的距离相等的所有点的坐标(用含m的式子表示).
)时,请直接写出到△ABD的三边所在直线的距离相等的所有点的坐标(用含m的式子表示).
解:(1)当m=时,抛物线C1:y=(x+)2.
∵抛物线C2的顶点D在抛物线C1上,且横坐标为a,
∴D(a,(a+)2).
∴抛物线C2:y=﹣(x﹣a)2+(a+)2 (I).
①∵OC=2,∴C(0,2).
∵点C在抛物线C2上,
∴﹣(0﹣a)2+(a+)2=2,
解得:a=,代入(I)式,
得抛物线C2的解析式为:y=﹣x2+x+2.
②在(I)式中,
令y=0,即:﹣(x﹣a)2+(a+)2=0,解得x=2a+或x=﹣,∴B(2a+,0);
令x=0,得:y=a+,∴C(0,a+).
设直线BC的解析式为y=kx+b,则有:
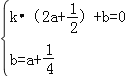 ,解得
,解得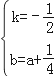 ,
,
∴直线BC的解析式为:y=﹣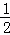 x+(a+
x+(a+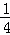 ).
).
假设存在满足条件的a值.
∵AP=BP,
∴点P在AB的垂直平分线上,即点P在C2的对称轴上;
∵点B与点C到直线OP的距离之和≤BC,只有OP⊥BC时等号成立,
∴OP⊥BC.
如答图1所示,设C2对称轴x=a(a>0)与BC交于点P,与x轴交于点E,
则OP⊥BC,OE=a.
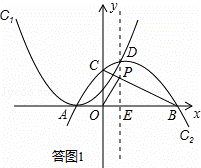
∵点P在直线BC上,∴∴P(a,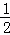 a+
a+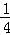 ),PE=
),PE=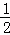 a+
a+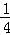 .
.
∵tan∠EOP=tan∠BCO=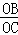 =
=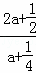 =2,
=2,
∴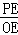 =
=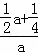 =2,
=2,
解得:a=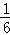 .
.
∴存在a=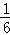 ,使得线段BC上有一点P,满足点B与点C到直线OP的距离之和最大且AP=BP
,使得线段BC上有一点P,满足点B与点C到直线OP的距离之和最大且AP=BP
(3)∵抛物线C2的顶点D在抛物线C1上,且横坐标为a,
∴D(a,(a+m)2).
∴抛物线C2:y=﹣(x﹣a)2+(a+m)2.
令y=0,即﹣(x﹣a)2+(a+m)2=0,解得:x1=2a+m,x2=﹣m,∴B(2a+m,0).
∵OB=2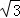 ﹣m,∴2a+m=2
﹣m,∴2a+m=2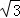 ﹣m,∴a=
﹣m,∴a=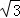 ﹣m.
﹣m.
∴D(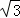 ﹣m,3).
﹣m,3).
AB=OB+OA=2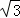 ﹣m+m=2
﹣m+m=2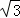 .
.
如答图2所示,设对称轴与x轴交于点E,则DE=3,BE=AB=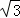 ,OE=OB﹣BE=
,OE=OB﹣BE=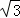 ﹣
﹣ m.
m.

∵tan∠ABD=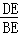 =
=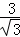 =
=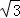 ,∴∠ABD=60°.
,∴∠ABD=60°.
又∵AD=BD,∴△ABD为等边三角形.
作∠ABD的平分线,交DE于点P1,则P1E=BE•tan30°= •
•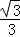 =1,
=1,
∴P1( ﹣m,1);
﹣m,1);
在△ABD形外,依次作各个外角的平分线,它们相交于点P2、P3、P4.
在Rt△BEP2中,P2E=BE•tan60°= •
• =3,
=3,
∴P2( ﹣m,﹣3);
﹣m,﹣3);
易知△ADP3、△BDP4均为等边三角形,∴DP3=DP4=AB=2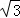 ,且P3P4∥x轴.
,且P3P4∥x轴.
∴P3(﹣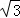 ﹣m,3)、P4(3
﹣m,3)、P4(3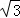 ﹣m,3).
﹣m,3).
综上所述,到△ABD的三边所在直线的距离相等的所有点有4个,
其坐标为:P1(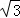 ﹣m,1),P2(
﹣m,1),P2(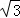 ﹣m,﹣3),P3(﹣
﹣m,﹣3),P3(﹣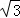 ﹣m,3),P4(3
﹣m,3),P4(3 ﹣m,3).
﹣m,3).


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:初中数学 来源: 题型:
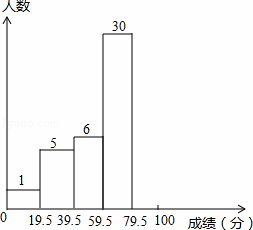
如图是某数学兴趣小组参加“奥数”后所得成绩绘制成的频数,频率分布表和频数分布直方图.请你根据图表提供的信息,解答下列问题(成绩取整数,满分为100分)
| 分组 | 0﹣19.5 | 19.5﹣39.5 | 39.5﹣59.5 | 59.5﹣79.5 | 79.5﹣100 | 合计 |
| 频数 | 1 | 5 | 6 | 30 | b | 50 |
| 频率 | 0.02 | a | 0.12 | 0.60 | 0.16 | 1 |
(1)频数、频率分布表中a= ,b= .
(2)补全频数分布直方图.
(3)若在80分以上的小组成员中选3人参加下一轮竞赛,小明本次竞赛的成绩为90分,他被选中的概率是多少?
(4)从该图中你还能获得哪些数学信息?(填写一条即可 )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
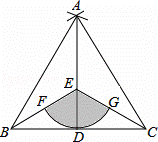
如图,点D是线段BC的中点,分别以点B,C为圆心,BC长为半径画弧,两弧 相交于点A,连接AB,AC,AD,点E为AD上一点,连接BE,CE.
相交于点A,连接AB,AC,AD,点E为AD上一点,连接BE,CE.
(1)求证:BE=CE;
(2)以点E为圆心,ED长为半径画弧,分别交BE,CE于点F,G.若BC=4,∠EBD=30°,求图中阴影部分(扇形)的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
甲、乙两支仪仗队的队员人数相同,平均身高相同,身高的方差分别为S2甲=0.9,S2乙=1.1,则甲、乙两支仪仗队的队员身高更整齐的是 (填“甲”或“乙”).
查看答案和解析>>
科目:初中数学 来源: 题型:
将二次函数y=x2的图象向右平移1个单位,再向上平移2个单位后,所得图象的函数表达式是( )
|
| A. | y=(x﹣1)2+2 | B. | y=(x+1)2+2 | C. | y=(x﹣1)2﹣2 | D. | y=(x+1)2﹣2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com