
【题目】如图,抛物线![]() 的对称轴为直线x=
的对称轴为直线x=![]() ,与
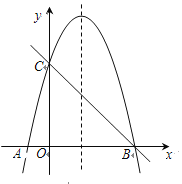
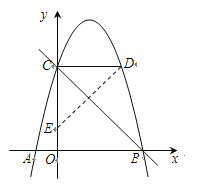
,与![]() 轴交于A,B两点,与y轴交于点C(0,4).(1)求抛物线的解析式,结合图象直接写出当0≤x≤4时y的取值范围;(2)已知点D(m,m+1)在第一象限的抛物线上,点D关于直线BC的对称点为点E,求点E的坐标.
轴交于A,B两点,与y轴交于点C(0,4).(1)求抛物线的解析式,结合图象直接写出当0≤x≤4时y的取值范围;(2)已知点D(m,m+1)在第一象限的抛物线上,点D关于直线BC的对称点为点E,求点E的坐标.
【答案】(1)、y=-![]() +3x+4;0≤y≤
+3x+4;0≤y≤![]() ;(2)、E(0,1)
;(2)、E(0,1)
【解析】
试题分析:(1)、首先将点C的坐标代入求出a的值,然后根据函数的对称轴求出b的值,从而得出抛物线的解析式,根据函数的性质求出y的取值范围;(2)、首先将点D的坐标代入解析式求出点D的坐标,然后根据轴对称性求出点E的坐标.
试题解析:(1)、将C(0,4)代入![]() 中得a=-1
中得a=-1
又∵对称轴为直线x=![]() ,∴
,∴![]() ,得b=3. 抛物线的解析式为
,得b=3. 抛物线的解析式为![]() .
.
当0≤x≤4时y的取值范围是0≤y≤![]() .
.
(2)、∵点D(m,m+1)在抛物线上,∴m+1=![]() .
.
∴m=-1或m=3. ∵点D在第一象限,∴点D的坐标为(3,4)
又∵C(0,4),所以CD∥AB,且CD=3. 由![]() 得B(4,0)
得B(4,0)
∴∠OCB=∠DCB=45°. ∴点E在![]() 轴上,且CE=CD=3,∴OE=1. 即点E的坐标为(0,1).
轴上,且CE=CD=3,∴OE=1. 即点E的坐标为(0,1).


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+mx+(m-1)与x轴交于点A(x1,0),B(x2,0),x1<x2,与y轴交于点C(0,c),且满足x12+x22+x1x2=7.
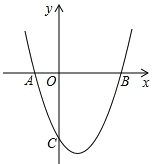
(1)求抛物线的解析式;
(2)在抛物线上能不能找到一点P,使∠POC=∠PCO?若能,请求出点P的坐标;若不能,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“神州五号”载人飞船绕地球飞行14圈,共飞行590200km,这个飞行距离用科学计数法表示为( )
A. 59.02×104km B. 0.5902×106km C. 5.902×105km D. 5.902×104km
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于用四舍五入法得到的近似数4.609万,下列说法中正确的是( )
A. 它精确到千分位 B. 它精确到0.01
C. 它精确到万位 D. 它精确到十位
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com