
【题目】如图,抛物线y=x2+mx+(m-1)与x轴交于点A(x1,0),B(x2,0),x1<x2,与y轴交于点C(0,c),且满足x12+x22+x1x2=7.
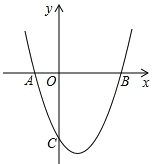
(1)求抛物线的解析式;
(2)在抛物线上能不能找到一点P,使∠POC=∠PCO?若能,请求出点P的坐标;若不能,请说明理由
【答案】(1)y=x2-2x-3;(2)能,点P的坐标是(![]() ,-
,-![]() ),(
),(![]() ,-
,-![]() )
)
【解析】
试题分析:(1)利用根与系数的关系,等式x12+x22+x1x2=7.由一元二次方程根与系数的关系,得x1+x2=-m,x1x2=m-1.代入等式,即可求得m的值,从而求得解析式.
(2)根据线段的垂直平分线上的点到两端点的距离相等,求得P点的纵坐标,代入抛物线的解析式即可求得.
试题解析:(1)依题意:x1+x2=-m,x1x2=m-1,
∵x12+x22+x1x2=7,
∴(x1+x2)2-x1x2=7,
∴(-m)2-(m-1)=7,
即m2-m-6=0,
解得m1=-2,m2=3,
∵c=m-1<0,∴m=3不合题意
∴m=-2
抛物线的解析式是y=x2-2x-3;
(2)能
如图,设P是抛物线上的一点,连接PO,PC,过点P作y轴的垂线,垂足为D.
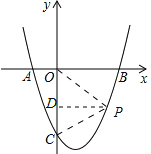
若∠POC=∠PCO
则PD应是线段OC的垂直平分线
∵C的坐标为(0,-3)
∴D的坐标为(0,-![]() )
)
∴P的纵坐标应是-![]()
令x2-2x-3=-![]() ,解得,x1=
,解得,x1=![]() ,x2=
,x2=![]()
因此所求点P的坐标是(![]() ,-
,-![]() ),(
),(![]() ,-
,-![]() )
)


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD于点E,DA平分∠BDE.
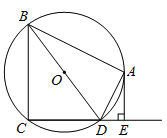
(1)求证:AE是⊙O的切线;
(2)如果AB=4,AE=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l平行x轴,交y轴于点A,第一象限内的点B在l上,连结OB,动点P满足∠APQ=90°,PQ交x轴于点C.
(1)当动点P与点B重合时,若点B的坐标是(2,1),求PA的长.
(2)当动点P在线段OB的延长线上时,若点A的纵坐标与点B的横坐标相等,求PA:PC的值.
(3)在(2)的条件下,已知AB=3,OB:BP=3:1,求四边形AOCP的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
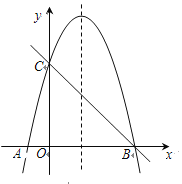
【题目】如图,抛物线![]() 的对称轴为直线x=
的对称轴为直线x=![]() ,与
,与![]() 轴交于A,B两点,与y轴交于点C(0,4).(1)求抛物线的解析式,结合图象直接写出当0≤x≤4时y的取值范围;(2)已知点D(m,m+1)在第一象限的抛物线上,点D关于直线BC的对称点为点E,求点E的坐标.
轴交于A,B两点,与y轴交于点C(0,4).(1)求抛物线的解析式,结合图象直接写出当0≤x≤4时y的取值范围;(2)已知点D(m,m+1)在第一象限的抛物线上,点D关于直线BC的对称点为点E,求点E的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com