
 在“美丽的滕州,清洁乡村”活动中,光明村村长提出了两种购买垃圾桶方案;
在“美丽的滕州,清洁乡村”活动中,光明村村长提出了两种购买垃圾桶方案;分析 (1)根据总费用=购买垃圾桶的费用+每月的垃圾处理费用×月份数,即可求出y1、y2与x的函数关系式;
(2)根据一次函数的性质,运用两点法即可画出函数y1、y2的图象;
(3)观察图象可知:当使用时间为9个月时,方案1省钱;当该村拿出4000元的费用时,方案2使用的时间更长.
解答 解:(1)由题意,得y1=250x+3000,y2=500x+1000;
(2)如图所示: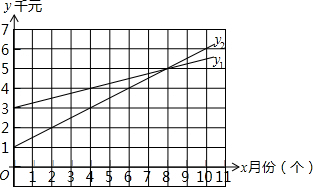
(3)由图象可知:①当使用时间为9个月时,直线y1落在直线y2的下方,y1<y2,即方案1省钱;
②当该村拿出4000元的费用时,x1=4,x2=6,即方案2使用的时间更长.
点评 本题主要考查利用一次函数的模型解决实际问题的能力.解题的关键是根据题意列出函数关系式,再结合图象求解.注意数形结合思想的运用.


 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:选择题
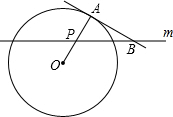 如图,A点在半径为2的⊙O上,过线段OA上的一点P作直线m,与⊙O过A点的切线交于点B,且∠APB=60°,设OP=x,则△PAB的面积y关于x的函数图象大致是( )
如图,A点在半径为2的⊙O上,过线段OA上的一点P作直线m,与⊙O过A点的切线交于点B,且∠APB=60°,设OP=x,则△PAB的面积y关于x的函数图象大致是( )| A. | 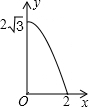 | B. | 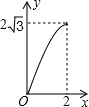 | C. | 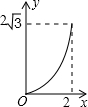 | D. | 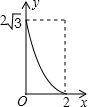 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
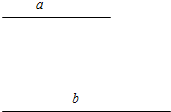 画图:已知线段a、b.
画图:已知线段a、b.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
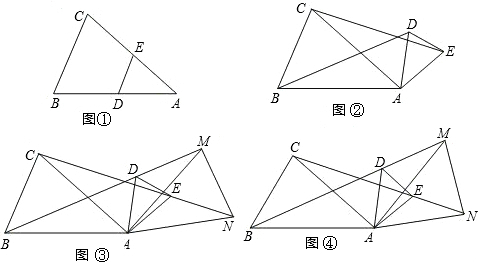
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
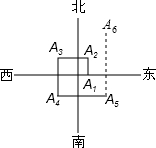 如图,一个机器人从O点出发,向正东方向走3m,到达A1点,再向正北走6m到达A2点,再向正西走9m到达A3点,再向正南走12m,到达A4点,再向正东方向走15m到达A5点,按如此规律走下去,当机器人走到A6点时,A6点的坐标是( )
如图,一个机器人从O点出发,向正东方向走3m,到达A1点,再向正北走6m到达A2点,再向正西走9m到达A3点,再向正南走12m,到达A4点,再向正东方向走15m到达A5点,按如此规律走下去,当机器人走到A6点时,A6点的坐标是( )| A. | (9,12) | B. | (9,9) | C. | (9,6) | D. | (9,3) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3.3192×108 | B. | 3.3192×109 | C. | 3.3192×1010 | D. | 3.3192×1011 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com