
分析 分类讨论:当EC=EF,如图1,证明△AEC为等腰三角形,得到AE=AC=20;当FC=FE,如图2,证明△EAC∽△CAB,利用相似比计算AE的长.
解答 解:当EC=EF,如图1,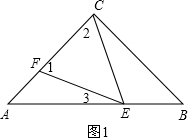
∴∠1=∠2,
∵AB=AC=20,
∴∠A=∠B,
∵∠CEF=∠B,
∴∠A=∠CEF,
∵∠1=∠A+∠3,
∴∠1=∠CEF+∠3=∠AEC,
∴∠AEC=∠2,
∴AE=AC=20;
当FC=FE,如图2,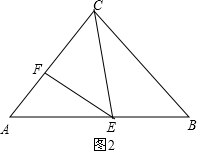
∴∠ECF=∠CEF,
∵∠CEF=∠B=∠A,
∴∠A=∠B=∠ACE,
∴△EAC∽△CAB,
∴$\frac{AE}{CA}$=$\frac{CA}{AB}$,即$\frac{AE}{20}$=$\frac{20}{24}$,
∴AE=$\frac{50}{3}$,
综上所述,AE的长为20或$\frac{50}{3}$.
故答案为20或$\frac{50}{3}$.
点评 本题考查了相似三角形的判定与性质:判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形.也考查了等腰三角形的判定与性质和分类讨论思想的应用.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在“美丽的滕州,清洁乡村”活动中,光明村村长提出了两种购买垃圾桶方案;
在“美丽的滕州,清洁乡村”活动中,光明村村长提出了两种购买垃圾桶方案;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
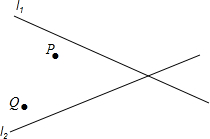 如图,邳州电讯公司要修建一座信号发射塔,按设计要求,发射塔到两城镇P、Q的距离相等,并且到两条公路l1、l2的距离也相等,请你帮助设计员在图中画出发射塔的位置(使用尺规作图,保留作图痕迹).
如图,邳州电讯公司要修建一座信号发射塔,按设计要求,发射塔到两城镇P、Q的距离相等,并且到两条公路l1、l2的距离也相等,请你帮助设计员在图中画出发射塔的位置(使用尺规作图,保留作图痕迹).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2.14×103 | B. | 2.14×104 | C. | 21.4×102 | D. | 0.214×104 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
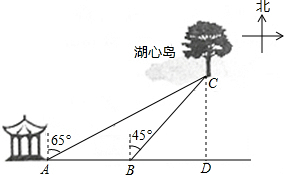 如图,小明想用所学的知识来测量湖心岛上的迎宾槐与岸上的凉亭间的距离,如图,小明想用所学的知识来测量湖心岛上的迎宾槐与岸上的凉亭间的距离,他先在湖岸上的凉亭A处测得湖心岛上的迎宾槐C处位于北偏东65°方向,然后,他从凉亭A处沿湖岸向正东方向走了100米到B处,测得湖心岛上的迎宾槐C处位于北偏东45°方向(点A、B、C在同一水平面上).请你利用小明测得的相关数据,求湖心岛上的迎宾槐C处与湖岸上的凉亭A处之间的距离(结果精确到1米).
如图,小明想用所学的知识来测量湖心岛上的迎宾槐与岸上的凉亭间的距离,如图,小明想用所学的知识来测量湖心岛上的迎宾槐与岸上的凉亭间的距离,他先在湖岸上的凉亭A处测得湖心岛上的迎宾槐C处位于北偏东65°方向,然后,他从凉亭A处沿湖岸向正东方向走了100米到B处,测得湖心岛上的迎宾槐C处位于北偏东45°方向(点A、B、C在同一水平面上).请你利用小明测得的相关数据,求湖心岛上的迎宾槐C处与湖岸上的凉亭A处之间的距离(结果精确到1米).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com