
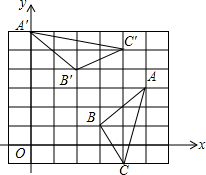
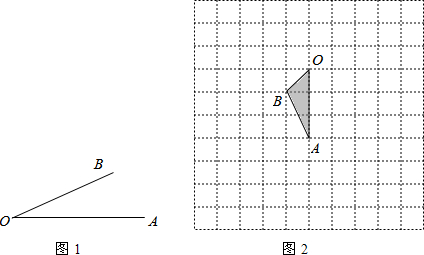
 如图,将△ABC绕点P逆时针旋转90°得到△A′B′C,则点P的坐标是( )
如图,将△ABC绕点P逆时针旋转90°得到△A′B′C,则点P的坐标是( )| A. | (1,1) | B. | (2,1) | C. | (1,2) | D. | (1,3) |
分析 先根据旋转的性质得到点A的对应点为点A′,点B的对应点为点B′,再根据旋转的性质得到旋转中心在线段AA′的垂直平分线,也在线段BB′的垂直平分线,即两垂直平分线的交点为旋转中心.
解答 解:∵将△ABC以某点为旋转中心,顺时针旋转90°得到△A′B′C′,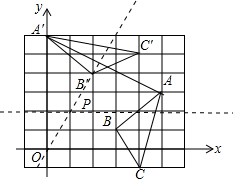
∴点A的对应点为点A′,点C的对应点为点C′,
作线段AA′和CC′的垂直平分线,它们的交点为P(1,2),
∴旋转中心的坐标为(1,2).
故选:C.
点评 本题考查了坐标与图形变化-旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:初中数学 来源: 题型:选择题
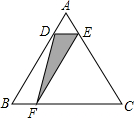 如图,在等边△ABC中,点D是AB边上的动点,过点作DE∥BC交边AC于点E,过点作EF∥AB交边BC于点F.连结DF,设动点D从点A出发沿AB匀速向点B运动,运动时间为t,则在整个运动过程中,△DEF的面积S与运动时间t的大致图象是( )
如图,在等边△ABC中,点D是AB边上的动点,过点作DE∥BC交边AC于点E,过点作EF∥AB交边BC于点F.连结DF,设动点D从点A出发沿AB匀速向点B运动,运动时间为t,则在整个运动过程中,△DEF的面积S与运动时间t的大致图象是( )| A. | 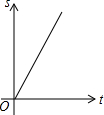 | B. | 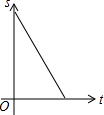 | C. | 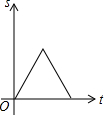 | D. | 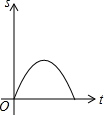 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
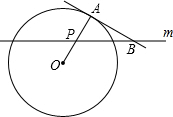 如图,A点在半径为2的⊙O上,过线段OA上的一点P作直线m,与⊙O过A点的切线交于点B,且∠APB=60°,设OP=x,则△PAB的面积y关于x的函数图象大致是( )
如图,A点在半径为2的⊙O上,过线段OA上的一点P作直线m,与⊙O过A点的切线交于点B,且∠APB=60°,设OP=x,则△PAB的面积y关于x的函数图象大致是( )| A. | 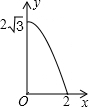 | B. | 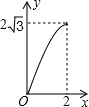 | C. | 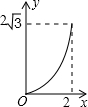 | D. | 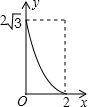 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
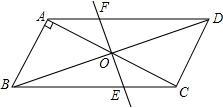 已知,如图?ABCD中,AB⊥AC,AB=1,BC=$\sqrt{5}$,对角线AC、BD交于0点,将直线AC绕点0顺时针旋转,分别交BC、AD于点E、F
已知,如图?ABCD中,AB⊥AC,AB=1,BC=$\sqrt{5}$,对角线AC、BD交于0点,将直线AC绕点0顺时针旋转,分别交BC、AD于点E、F查看答案和解析>>
科目:初中数学 来源: 题型:解答题
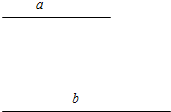 画图:已知线段a、b.
画图:已知线段a、b.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3×22012 | B. | 24025 | C. | -22012 | D. | ($\frac{1}{2}$)2012 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com