
 如图,过正方形ABCD的对角线BD上一点P,作PE⊥BC于点E,PF⊥CD于点F,求证:AP=EF.
如图,过正方形ABCD的对角线BD上一点P,作PE⊥BC于点E,PF⊥CD于点F,求证:AP=EF.  世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 物体质量x/千克 0 1 2 3 4 5… |
| 弹簧长度y/厘米 10 10.5 11 11.5 12 12.5… |
| A. | x与y都是变量,其中x是自变量,y是因变量 | |
| B. | 弹簧不挂重物时的长度为0厘米 | |
| C. | 在弹簧范围内,所挂物体质量为7千克时,弹簧长度为13.5厘米 | |
| D. | 在弹簧范围内,所挂物体质量每增加1千克弹簧长度增加0.5厘米 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图1、图2都是由8个一样的小长方形拼(围)成的大矩形,且图2中的明影部分(小矩形)的面积为1cm2.则小长方形的长为( )
如图1、图2都是由8个一样的小长方形拼(围)成的大矩形,且图2中的明影部分(小矩形)的面积为1cm2.则小长方形的长为( )| A. | 5 | B. | 3 | C. | 7 | D. | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
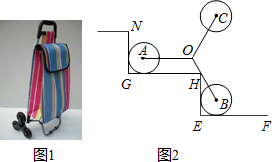 如图所示是装有三个小轮的手拉车在“爬”楼梯时的侧面示意图,定长的轮架杆OA,OB,OC抽象为线段,有OA=OB=OC,且∠AOB=120°.折线NG-GH-HE-EF表示楼梯,GH,EF是水平线,NG,HE是铅垂线,半径相等的小轮子⊙A,⊙B与楼梯两边都相切,且AO∥GH.如图2,若点H在线段OB时,则$\frac{BH}{OH}$的值是$\sqrt{3}$.
如图所示是装有三个小轮的手拉车在“爬”楼梯时的侧面示意图,定长的轮架杆OA,OB,OC抽象为线段,有OA=OB=OC,且∠AOB=120°.折线NG-GH-HE-EF表示楼梯,GH,EF是水平线,NG,HE是铅垂线,半径相等的小轮子⊙A,⊙B与楼梯两边都相切,且AO∥GH.如图2,若点H在线段OB时,则$\frac{BH}{OH}$的值是$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com