练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，矩形ABCD中，对角线AC与BD相交于点O，P为AD上的动点，过点P作PM⊥AC，PN⊥BD，垂足分别为M、N，若AB=m，BC=n，则PM+PN=（　　）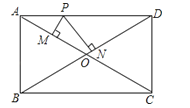

    A.
    B.
    C.
    D.

    【答案】C
    【解析】解：连接OP，如图所示：
    ∵四边形ABCD是矩形，
    ∴∠ABC=90°，OA=AC，OD=BD，AC=BD，
    ∴OA=OD，AC= ，
    ∴OA=OD= ，
    ∵△OAP的面积+△ODP的面积=△AOD的面积=矩形ABCD的面积，
    即OAPM+ODPN=OA（PM+PN）=ABBC=mn，
    ∴PM+PN== ，
    故选：C．

    连接OP，由矩形的性质得出OA=OD，∠ABC=90°，由勾股定理求出AC，得出OA，由△OAP的面积+△ODP的面积=矩形ABCD的面积，即可得出结果．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】下列运算正确的是（　　）

    A. （﹣a2）3＝a6B. a2a3＝a6C. （﹣ab）2＝a2bD. 2a6÷a3＝2a3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）先化简，再求值：÷（﹣），其中x=+ ， y=﹣ ．
    （2）在数轴上画出表示的点． （要求画出作图痕迹）

    （3）如图，左边是由两个边长为2的小正方形组成，沿着图中虚线剪开，可以拼成右边的大正方形，求大正方形的边长．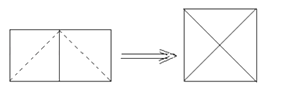

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，AB=AC，AD是∠BAC的角平分线，点O为AB的中点，连接DO并延长到点E，使OE=OD，连接AE，BE．
    （1）求证：四边形AEBD是矩形；
    （2）当△ABC满足什么条件时，矩形AEBD是正方形，并说明理由．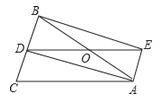

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，把△ABC纸片沿DE折叠，当点A落在四边形BCDE内部时，则∠A与∠1+∠2之间有一种数量关系始终保持不变．请试着找一找这个规律，你发现的规律是（ ）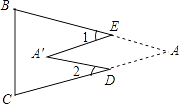
    A.∠A=∠1+∠2
    B.2∠A=∠1+∠2
    C.3∠A=2∠1+∠2
    D.3∠A=2（∠1+∠2）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，把△ABC纸片沿DE折叠，当点A落在四边形BCDE内部时，则∠A与∠1+∠2之间有一种数量关系始终保持不变，请试着找一找这个规律，这个规律是（ ）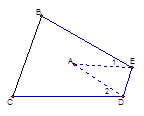

    A.∠A=∠1+∠2
    B.2∠A=∠1+∠2
    C.3∠A=2∠1+∠2
    D.3∠A=2（∠1+∠2）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，四边形ABCD是平行四边形，AC、BD交于点O，∠1=∠2．
    （1）求证：四边形ABCD是矩形；
    （2）若∠BOC=120°，AB=4cm，求四边形ABCD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若a－b＝3，ab＝2，则a2b－ab2＝ ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若a﹣b=2，3a+2b=3，则3a（a﹣b）+2b（a﹣b）=___．

    查看答案和解析>>

    同步练习册答案