
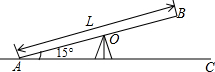
 (2010•来宾)儿童活动乐园中的跷跷板AB的支撑架位于板的中点O处(如图),一端压下与地面接触于点A,翘起的板与地面AC所成的最大角度为15°,为了安全,要求此时翘起一端的端点B离地面的最大高度是0.8米,最小高度是0.6米,试求出跷跷板的长度L的取值范围(要求列不等式(组)求解,精确到0.01米).(参考数据:sin15°≈0.259,cos15°≈0.966,tan15°≈0.268)
(2010•来宾)儿童活动乐园中的跷跷板AB的支撑架位于板的中点O处(如图),一端压下与地面接触于点A,翘起的板与地面AC所成的最大角度为15°,为了安全,要求此时翘起一端的端点B离地面的最大高度是0.8米,最小高度是0.6米,试求出跷跷板的长度L的取值范围(要求列不等式(组)求解,精确到0.01米).(参考数据:sin15°≈0.259,cos15°≈0.966,tan15°≈0.268)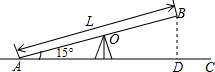 解:设跷跷板长x米,过点B作BD⊥AC于点D.
解:设跷跷板长x米,过点B作BD⊥AC于点D.

科目:初中数学 来源: 题型:
 (2010•来宾)已知矩形OABC的顶点O在平面直角坐标系的原点,边OA、OC分别在x、y轴的正半轴上,且OA=3cm,OC=4cm,点M从点A出发沿AB向终点B运动,点N从点C出发沿CA向终点A运动,点M、N同时出发,且运动的速度均为1cm/秒,当其中一个点到达终点时,另一点即停止运动.设运动的时间为t秒.
(2010•来宾)已知矩形OABC的顶点O在平面直角坐标系的原点,边OA、OC分别在x、y轴的正半轴上,且OA=3cm,OC=4cm,点M从点A出发沿AB向终点B运动,点N从点C出发沿CA向终点A运动,点M、N同时出发,且运动的速度均为1cm/秒,当其中一个点到达终点时,另一点即停止运动.设运动的时间为t秒.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com