练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】写出一个一元一次方程，要求：解此方程时第一步必须是利用合并同类项法则合并同类项．我写的方程为_____．

    【答案】x+3x＝5（答案不唯一）．

    【解析】

    同类项是指具有相同的字母,并且相同字母的指数也相同，据此即可解题.

    解：这个方程可以是x+3x＝5（答案不唯一）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图所示，∠E=∠F，∠B=∠C，AE=AF，以下结论：①∠FAN=∠EAM；②EM=FN；③△ACN≌△ABM；④CD=DN．其中正确的有（　　）

    A.1个
    B.2个
    C.3个
    D.4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图在△ABC中，CD是高，点E、F、G分别在BC、AB、AC上，且EF⊥AB，∠1=∠2，试判断DG与BC的位置关系？并说明理由。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若点(－1，m)和点(1，n)在一次函数y＝－3x＋6的图像上，则m______n(填“>”“<”或“＝”)．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

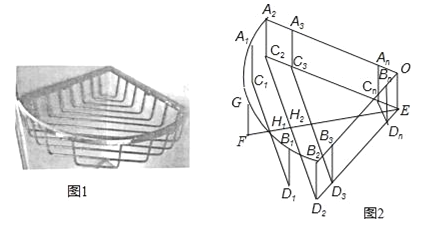
    【题目】如图1是一个用铁丝围成的篮框，我们来仿制一个类似的柱体形篮框．如图2，它是由一个半径为r、圆心角90°的扇形A2OB2，矩形A2C2EO、B2D2EO，及若干个缺一边的矩形状框A1C1D1B1、A2C2D2B2、…、AnBnCnDn，OEFG围成，其中A1、G、B1在上，A2、A3…、An与B2、B3、…Bn分别在半径OA2和OB2上，C2、C3、…、Cn和D2、D3…Dn分别在EC2和ED2上，EF⊥C2D2于H2，C1D1⊥EF于H1，FH1=H1H2=d，C1D1、C2D2、C3D3、CnDn依次等距离平行排放（最后一个矩形状框的边CnDn与点E间的距离应不超过d），A1C1∥A2C2∥A3C3∥…∥AnCn．

    （1）求d的值；

    （2）问：CnDn与点E间的距离能否等于d？如果能，求出这样的n的值，如果不能，那么它们之间的距离是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，对称轴为直线x=的抛物线经过B（2，0）、C（0，4）两点，抛物线与x轴的另一交点为A．

    （1）求抛物线的解析式；

    （2）若点P为第一象限内抛物线上的一点，设四边形COBP的面积为S，求S的最大值；

    （3）如图2，若M是线段BC上一动点，在x轴是否存在这样的点Q，使△MQC为等腰三角形且△MQB为直角三角形？若存在，求出点Q的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】a-b =a+（ ）
    A.-b
    B.b
    C.a
    D.-a

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解方程：1﹣（2x﹣5）＝7﹣3x．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线与x轴交于A、B两点，且B（1，0）

    （1）求抛物线的解析式和点A的坐标；

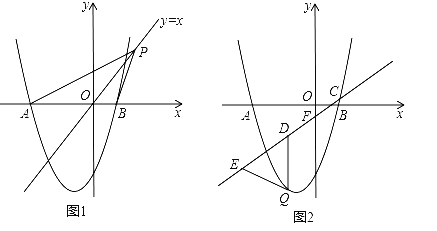
    （2）如图1，点P是直线y=x上的动点，当直线y=x平分∠APB时，求点P的坐标；

    （3）如图2，已知直线分别与x轴、y轴交于C、F两点，点Q是直线CF下方的抛物线上的一个动点，过点Q作y轴的平行线，交直线CF于点D，点E在线段CD的延长线上，连接QE．问：以QD为腰的等腰△QDE的面积是否存在最大值？若存在，请求出这个最大值；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案