
 如图,是一张矩形纸片,其中AB=1,BC=2,怎样折叠这张纸片,才能找到AB边上的黄金分割.
如图,是一张矩形纸片,其中AB=1,BC=2,怎样折叠这张纸片,才能找到AB边上的黄金分割. 分析 根据黄金分割点定义,只要求作线段BG=$\frac{\sqrt{5}-1}{2}$,由此思路即可解决问题.
解答 解:如图,在矩形ABCD中,连接BD,在DB上截取DE=DC=1,取BE中点F,
在BA上截取BG=BF,
则点G就是线段AB的黄金分割点.
理由:∵四边形ABCD是矩形,
∴∠BCD=90°,BD=$\sqrt{B{C}^{2}+C{D}^{2}}$=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
∵DE=DC=1,
∴BF=EF=$\frac{\sqrt{5}-1}{2}$,
∴BG=$\frac{\sqrt{5}-1}{2}$,
即BG=$\frac{\sqrt{5}-1}{2}$AB,
∴点G就是线段AB的黄金分割点.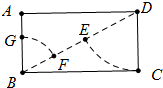
点评 本题考查黄金分割的定义,在线段AB上有一点C如果AC=$\frac{\sqrt{5}-1}{2}$AB,那么点C就是线段AB的黄金分割点,解题的关键是记住黄金分割点的定义找到$\sqrt{5}$这条线段,在作图问题中属于比较难的题目.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 某新建小区里安装了一架秋千,图是一个小孩荡秋千的侧面示意图,秋千的链子OA的长度为3米,秋千向两边摆动的最大角度相同,且最大角度的和∠BOC恰好为90°,则它摆至最高位置与最低位置的高度之差是(3-$\frac{3\sqrt{2}}{2}$)米.
某新建小区里安装了一架秋千,图是一个小孩荡秋千的侧面示意图,秋千的链子OA的长度为3米,秋千向两边摆动的最大角度相同,且最大角度的和∠BOC恰好为90°,则它摆至最高位置与最低位置的高度之差是(3-$\frac{3\sqrt{2}}{2}$)米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
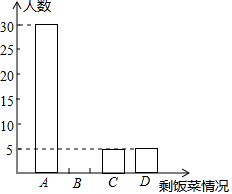 我市某中学积极开展“厉行勤俭节约,反对铺张浪费”的活动.为此,校学生会在全校范围内随机抽取了若干名学生就某日午饭浪费饭菜情况进行调查,调查内容分为四种:A.饭和菜全部吃完;B.有剩饭但菜吃完;C.饭吃完但菜有剩;D.饭和菜都有剩.学生会根据统计结果,绘制了如下统计表和统计图,根据所提供的信息回答下列问题:
我市某中学积极开展“厉行勤俭节约,反对铺张浪费”的活动.为此,校学生会在全校范围内随机抽取了若干名学生就某日午饭浪费饭菜情况进行调查,调查内容分为四种:A.饭和菜全部吃完;B.有剩饭但菜吃完;C.饭吃完但菜有剩;D.饭和菜都有剩.学生会根据统计结果,绘制了如下统计表和统计图,根据所提供的信息回答下列问题:| 选项 | 频数 | 频率 |
| A | 30 | m |
| B | n | 0.2 |
| C | 5 | 0.1 |
| D | 5 | 0.1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8$\sqrt{2}$cm | B. | 4$\sqrt{2}$cm | C. | 8$\sqrt{3}$cm | D. | 4$\sqrt{3}$cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com