
科目: 来源: 题型:填空题
查看答案和解析>>
科目: 来源: 题型:解答题
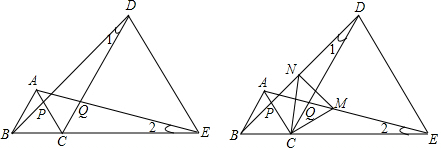
查看答案和解析>>
科目: 来源: 题型:解答题
 如图甲,有一个塔高40米,位于一座山上,在其下方有一个坡度i=1:1的斜坡,某一时刻,身高1.60米的同学小明测得自己的影子(在平地上)为0.8米,那么,此时这个塔在斜坡上的影子长为多少米?(可借用图形乙)
如图甲,有一个塔高40米,位于一座山上,在其下方有一个坡度i=1:1的斜坡,某一时刻,身高1.60米的同学小明测得自己的影子(在平地上)为0.8米,那么,此时这个塔在斜坡上的影子长为多少米?(可借用图形乙)查看答案和解析>>
科目: 来源: 题型:解答题
 阅读理解
阅读理解 解得
解得

查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com