练习册

  • 练习册
  • 试题
    相关习题
     0  16732  16740  16746  16750  16756  16758  16762  16768  16770  16776  16782  16786  16788  16792  16798  16800  16806  16810  16812  16816  16818  16822  16824  16826  16827  16828  16830  16831  16832  16834  16836  16840  16842  16846  16848  16852  16858  16860  16866  16870  16872  16876  16882  16888  16890  16896  16900  16902  16908  16912  16918  16926  366461 

    科目： 来源： 题型：解答题

    解方程组：数学公式．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    x2-2x=0的解是________

    查看答案和解析>>

    科目： 来源： 题型：解答题

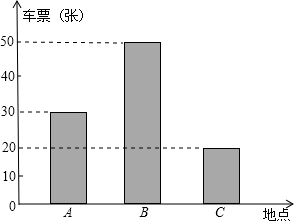    寒假假期，某学校准备组织部分学生到A、B、C三地参观学习．学校购买前往各地的车票种类和数量绘制成统计图，如图．根据统计图回答下列问题：
    （1）前往A地的车票有______张，前往C地的车票占全部车票的______%；
    （2）若学校决定采用随机抽取的方式把车票分配给100名学生，在看不到车票的条件下，每人抽取一张（每张车票的形状、大小、质地完全相同且充分洗匀），那么学生王小兵抽到去B地车票的概率为______；
    （3）若剩下最后一张车票时，学生张三、李四都想要，决定采用摸球的方法来确定，具体规则是：在一个不透明的袋子里装有四个分别标有数字1，2，3，4的小球，它们的形状、大小等完全相同，每人随机从袋子里摸出一个球，记下数字后放回袋子中，充分摇匀后再由第二个人摸出一球．若张三摸得的球上的数字比李四摸得的球上的数字大，车票给张三，否则给李四．”试用“列表法或画树形图”的方法分析，这个规则对双方是否公平？

    查看答案和解析>>

    科目： 来源： 题型：解答题

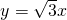    如图，直线l1分别交x轴、y轴于A、B两点，且AO=8，数学公式，与直线数学公式交于点C．平行于y轴的直线L2从原点O出发，以每秒1个单位长度的速度沿x轴向右平移，到C点时停止；l2分别交线段BC、OC、x轴于点D、E、P，以DE为边向左侧作等边△DEF，设直线l2的运动时间为t（秒）．
    （1）直接写出直线l1的解析式；
    （2）以D、E、O、F为顶点的多边形能否为梯形，若能，求出此时t的值；若不能，请说明理由；
    （3）设△DEF与△BCO重叠部分的面积为S（平方单位），试探究：S与t的函数关系式．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    如图所示，AB∥CD，若∠ABE=110°，∠DCE=40°，求∠BEC的度数．

    查看答案和解析>>

    科目： 来源： 题型：解答题

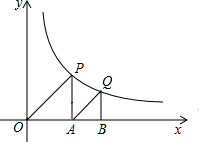    如图，△OAP、△ABQ均为等腰直角三角形，点P、Q在反比例函数图象上，直角顶点A、B均在x轴上，已知OP=数学公式．
    （1）求此反比例函数表达式；
    （2）求点Q的坐标．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    如图，这是某市一处十字路口立交桥的横断面在平面直角坐标系中的示意图，横断面的地平线为x轴，横断面的对称轴为y轴．桥拱的DGD′部分为一段抛物线，顶点G的高度为8米，AD和A′D′的两侧高为5.5米的支柱，OA和OA′为两个方向的汽车通行区，宽都为15米，线段CD和C′D′为两段对称的上桥斜坡，其坡度为1：4．
    （1）求桥拱DGD′所在抛物线的解析式及CC′的长；
    （2）BE和B′E′为支撑斜坡的立柱，其高都为4米，相应的AB和A′B′为两个方向的行人及非机动车通行区．试求AB和A′B′的宽；
    （3）按规定，汽车通过该桥下时，载货最高处和桥拱之间的距离不得小于0.4米．今有一大型运货汽车，装载某大型设备后，其宽为4米，车载大型设备的顶部与地面的距离均为7米．它能否从OA（或OA′）区域安全通过？请说明理由．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    已知二次函数的图象经过点（0，-3），且顶点坐标为（-1，-4）．
    （1）求该二次函数的解析式；
    （2）设该二次函数的图象与x轴的交点为A、B，与y轴的交点为C，求△ABC的面积．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    某农机租赁公司共有50台收割机，其中甲型20台、乙型30台，现将这50台联合收割机派往A、B两地区收割水稻，其中30台派往A地区，20台派往B地区，两地区与该农机公司商定的每天租赁价格如下表：
    每台甲型收割机的租金每台乙型收割机的租金
    A地区1800元1600元
    B地区1600元1200元
    （1）设派往A地区x台乙型联合收割机，租赁公司这50台联合收割机一天获得的租金为y元，求y关于x的函数关系式；
    （2）若使农机租赁公司这50台收割机一天所获租金不低于79600元，试写出满足条件的所有分派方案；
    （3）农机租赁公司拟出一个分派方案，使该公司50台收割机每天获得租金最高，并说明理由．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    已知抛物线的顶点坐标（2，3）且过点（3，4），求抛物线的解析式．

    查看答案和解析>>

    同步练习册答案