练习册

  • 练习册
  • 试题
    相关习题
     0  18105  18113  18119  18123  18129  18131  18135  18141  18143  18149  18155  18159  18161  18165  18171  18173  18179  18183  18185  18189  18191  18195  18197  18199  18200  18201  18203  18204  18205  18207  18209  18213  18215  18219  18221  18225  18231  18233  18239  18243  18245  18249  18255  18261  18263  18269  18273  18275  18281  18285  18291  18299  366461 

    科目： 来源： 题型：填空题

    为北京成功筹办2008年奥运会，顺义区准备对潮白河某水上工程进行改造，若请甲工程队单独做此工程需4个月完成，若请乙工程队单独做此工程需6个月完成，现在甲、乙两队先合作2个月，你猜乙工程队再单独做此工程需个月能完成？你能列出方程吗？
    分析：设________，等量关系：________；方程：________．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    为配合新课程的实施，某校举行了一次“应用与创新”知识竞赛，共有80名学生参加，为了了解本次成绩情况，对成绩作了如下统计
    组别分组频数频率
    149.5～59.560.075
    259.5～69.5
    369.5～79.50.375
    479.5～89.5220.275
    589.5～99.5100.125
    合计80
    （1）填写表格中空缺的部分．
    （2）如果这次竞赛的满分为100分，则这80名同学中有没有100分的同学？
    （3）根据表格绘制频数分布直方图．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    如图：有一轴截面为正三角形的圆锥形容器，内部盛水高度为10cm，放入一个球后，水面恰好与球相切，求球的半径．（圆锥的体积公式V=数学公式πR2h，其中R为底面半径，h为高线；球的体积公式V=数学公式πR3，其中R为球的半径）

    查看答案和解析>>

    科目： 来源： 题型：解答题

    填空或解答：点B、C、E在同一直线上，点A、D在直线CE的同侧，AB=AC，EC=ED，∠BAC=∠CED，直线AE、BD交于点F．
    （1）如图①，若∠BAC=60°，则∠AFB=______；如图②，若∠BAC=90°，则∠AFB=______；
    （2）如图③，若∠BAC=α，则∠AFB=______（用含α的式子表示）；
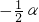    （3）将图③中的△ABC绕点C旋转（点F不与点A、B重合），得图④或图⑤．在图④中，∠AFB与∠α的数量关系是∠AFB=90°数学公式；在图⑤中，∠AFB与∠α的数量关系是______．请你任选其中一个结论证明．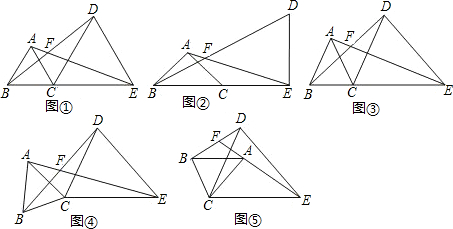

    查看答案和解析>>

    科目： 来源： 题型：解答题

    为了参加市教委举行的“争创绿色学校，美化校园环境”的活动，某区教委决定委托园林公司对所辖甲、乙两所学校进行校园绿化工作．已知甲校有如图1所示的矩形内阴影部分空地需铺设草坪，乙校有如图2所示的平行四边形内阴影部分空地需铺设草坪（图1，图2中数据单位均为“米”）．在A、B两地分别有同种草皮4500米2和2500米2出售，且售价一样．若园林公司向A、B两地购买草皮，其路程和运费单价表如下：
    甲校乙校
    路程（千米）运费单价（元） 路程（千米） 运费单价（元）　
    A地　　　　 20　　　　 0.3　　　　 10　　　　　 0.3
    B地　　　　 15　　　　 0.2　　　　 20　　　　　 0.2
    （注：运费单价表示每平方米草皮运送1千米所需要的人民币）
    （1）分别求出图1、图2的阴影部分面积；
    （2）若甲校从A地购买x米2的草皮（x取整数），因路程关系，甲校从A地购买的草皮数不超过甲校从B地购买的草皮数，乙校从B地购买的草皮数大于甲校从B地购买的草皮数的数学公式，那么甲校乙校从A，B两地购买草皮的方案有多少种？
    （3）在（2）的条件下，请你设计出总运费最低的草皮运送方案，并说明理由．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    正方形、线段、圆、角都是轴对称图形，它们分别有________、________、________、________条对称轴．

    查看答案和解析>>

    科目： 来源： 题型：解答题

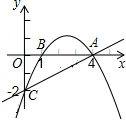    如图，已知抛物线经过A（4，0），B（1，0），C（0，-2）三点．
    （1）求该抛物线的解析式；
    （2）在直线AC上方的该抛物线上是否存在一点D，使得△DCA的面积最大？若存在，求出点D的坐标及△DCA面积的最大值；若不存在，请说明理由．
    （3）P是直线x=1右侧的该抛物线上一动点，过P作PM⊥x轴，垂足为M，是否存在P点，使得以A、P、M为顶点的三角形与△OAC相似？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    （1）在足球比赛中，当守门员远离球门时，进攻队员常常使用“吊射”的战术（把球高高地挑过守门员的头顶，射入球门）．一位球员在离对方球门30米的M处起脚吊射，假如球飞行的路线是一条抛物线，在离球门14米时，足球到达最大高度数学公式米，如图1，以球门底部为坐标原点建立坐标系，球门PQ的高度为2.44米，试通过计算说明，球是否会进入球门？
    （2）在（1）中，若守门员站在距球门2米远处，而守门员跳起后最多能摸到2.75米高处，他能否在空中截住这次吊射？
    （3）如图2，在另一次地面进攻中，假如守门员站在离球门中央2米远的A处防守，进攻队员在离球门中央12米的B处，以120千米/小时的球速起脚射门，射向球门的立柱C，球门的宽度CD为7.2米，而守门员防守的最远水平距离S（米）与时间t（秒）之间的函数关系式为S=10t，问守门员能否挡住这次射门？
    （4）在（3）的条件下，∠EAG区域为守门员的截球区域，试估计∠EAG的最大值（精确到0.1°）．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    用一不透明袋装有2个红球，3个黄球，除颜色不同外，其它特征均相同．
    （1）有放回地连续摸出两个球，两个球颜色相同的概率是多少？
    （2）无放回地连续摸出两个球，两个球颜色不相同的概率是多少？请你用列举法（列表或画树状图）加以分析说明．

    查看答案和解析>>

    科目： 来源： 题型：解答题

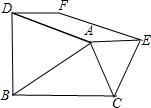    如图，以△ABC的边AB、AC为边的等边三角ABD和等边三角形ACE，四边形ADFE是平行四边形．
    （1）当∠BAC满足什么条件时，四边形ADFE是矩形；
    （2）当∠BAC满足什么条件时，平行四边形ADFE不存在；
    （3）当△ABC分别满足什么条件时，平行四边形ADFE是菱形，正方形？

    查看答案和解析>>

    同步练习册答案