
科目: 来源: 题型:
【题目】数轴上两点间的距离等于这两点所对应的数的差的绝对值.例:如图所示,点A、B在数轴上分别对应的数为a、b,则A、B两点间的距离表示为|AB|=|a﹣b|.
![]()
根据以上知识解题:
(1)若数轴上两点A、B表示的数为x、﹣1,
①A、B之间的距离可用含x的式子表示为 ;
②若该两点之间的距离为2,那么x值为 .
(2)|x+1|+|x﹣2|的最小值为 ,此时x的取值是 ;
(3)已知(|x+1|+|x﹣2|)(|y﹣3|+|y+2|)=15,求x﹣2y的最大值 和最小值 .
查看答案和解析>>
科目: 来源: 题型:
【题目】将连续的奇数1、3、5、7、9,……排成如下的数表:
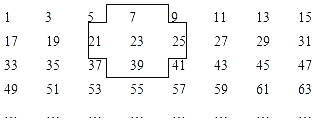
(1)十字框中的5个数的和与中间的数23有什么关系?若将十字框上下左右平移,可框住另外5个数,这5个数还有这种规律吗?
(2)设十字框中中间的数为a,用含a的式子表示十字框中的其他四个数;
(3)十字框中的5个数的和能等于2018吗?若能,请写出这5个数;若不能,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】计算:
(1)5![]() ﹣(﹣2
﹣(﹣2![]() )+(﹣3
)+(﹣3![]() )﹣(+4
)﹣(+4![]() )
)
(2)(﹣81)÷![]() ×
×![]() ÷(﹣
÷(﹣![]() )
)
(3)(﹣![]() )×(﹣
)×(﹣![]() )+(﹣
)+(﹣![]() )×(+
)×(+![]() )
)
(4)﹣14+|(﹣2)3﹣10|﹣(﹣3)÷(﹣1)2017
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线AB分别交y轴、x轴于A、B两点,OA=2,tan∠ABO= ![]() ,抛物线y=﹣x2+bx+c过A、B两点.
,抛物线y=﹣x2+bx+c过A、B两点.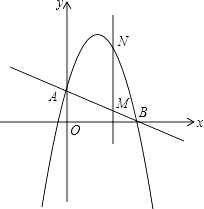
(1)求直线AB和这个抛物线的解析式;
(2)设抛物线的顶点为D,求△ABD的面积;
(3)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N.求当t取何值时,MN的长度l有最大值?最大值是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知数轴上点A表示的数为10,点B在点A左边,且AB=18.动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
(1)写出数轴上点B表示的数,点P表示的数(用含t的代数式表示);
(2)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发.
①问点P运动多少秒时追上点Q?
②问点P运动多少秒时与点Q相距4个单位长度?并求出此时点P表示的数;
(3)若点P、Q以(2)中的速度同时分别从点A、B向右运动,同时点R从原点O以每秒7个单位的速度向右运动,是否存在常数m,使得2QR+3OP﹣mOR为定值,若存在请求出m值以及这个定值;若不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,OC是∠AOB内的一条射线,OD、OE分别平分∠AOB、∠AOC.
(1)若∠AOC=20°,∠AOB=110°,则∠BOC= °,∠DOE= °;
(2)若∠AOC=m°,∠AOB=n°(n>m),则∠BOC= °,∠DOE= °;
(3)猜想:∠DOE与∠BOC有怎样的数量关系?并说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.

(1)求证:△ABD是等腰三角形;
(2)若∠A=40°,求∠DBC的度数;
(3)若AE=6,△CBD的周长为20,求△ABC的周长.
查看答案和解析>>
科目: 来源: 题型:
【题目】为增强公民的节约意识,合理利用天然气资源,某市自1月1日起对市区民用管道天然气价格进行调整,实行阶梯式气价,调整后的收费价格如表所示:
每月用气量 | 单价(元/m3) |
不超出80m3的部分 | 2.5 |
超出80m3不超出130m3的部分 | a |
超出130m3的部分 | a+0.5 |
(1)若甲用户3月份用气125m3,缴费335元,求a的值;
(2)在(1)的条件下,若乙用户3月份缴费392元,则乙用户3月份的用气量是多少?
查看答案和解析>>
科目: 来源: 题型:
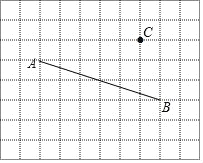
【题目】利用网格画图:
(1)过点C画AB的平行线;
(2)过点C画AB的垂线,垂足为E;
(3)连接CA、CB,在线段CA、CB、CE中, 线段最短,理由: ;
(4)点C到直线AB的距离是线段的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com