【题目】一艘渔船位于港口A的北偏东60°方向，距离港口20海里B处，它沿北偏西37°方向航行至C处突然出现故障，在C处等待救援，B，C之间的距离为10海里，救援船从港口A出发20分钟到达C处，求救援的艇的航行速度．（sin37°≈0.6，cos37°≈0.8， ≈1.732，结果取整数）

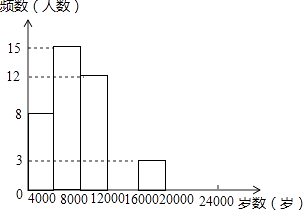
请根据以上信息，解答下列问题：
（1）写出a，b，c，d的值并补全频数分布直方图；
（2）本市约有37800名教师，用调查的样本数据估计日行走步数超过12000步（包含12000步）的教师有多少名？
（3）若在50名被调查的教师中，选取日行走步数超过16000步（包含16000步的两名教师与大家分享心得，求被选取的两名教师恰好都在20000步（包含20000步）以上的概率．

【题目】如图，四边形ABCD是平行四边形，E，F是对角线BD上的两点，且BF=ED，求证：AE∥CF．

【题目】如图，抛物线y=ax2+bx+c过点（﹣1，0），且对称轴为直线x=1，有下列结论： ①abc＜0；②10a+3b+c＞0；③抛物线经过点（4，y1）与点（﹣3，y2），则y1＞y2；④无论a，b，c取何值，抛物线都经过同一个点（﹣ ，0）；⑤am2+bm+a≥0，其中所有正确的结论是 ．

【题目】如图，点A（a，3），B（b，1）都在双曲线y= 上，点C，D，分别是x轴，y轴上的动点，则四边形ABCD周长的最小值为（ ）

A.
B.
C.
D.

【题目】如图，在矩形ABCD中，点F在AD上，点E在BC上，把这个矩形沿EF折叠后，使点D恰好落在BC边上的G点处，若矩形面积为4 且∠AFG=60°，GE=2BG，则折痕EF的长为（ ）
A.1
B.
C.2
D.

【题目】如图1，△ABC是等腰直角三角形，四边形ADEF是正方形，D、F分别在AB、AC边上，此时BD=CF，BD⊥CF成立．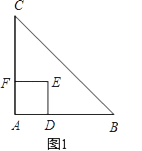
（1）当正方形ADEF绕点A逆时针旋转θ（0°＜θ＜90°）时，如图2，BD=CF成立吗？若成立，请证明；若不成立，请说明理由．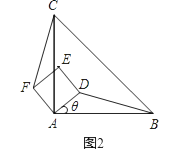
（2）当正方形ADEF绕点A逆时针旋转45°时，如图3，延长BD交CF于点G．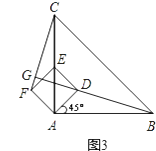
①求证：BD⊥CF；
②当AB=4，AD= 时，求线段BG的长．

【题目】若两个二次函数图象的顶点相同，开口大小相同，但开口方向相反，则称这两个二次函数为“对称二次函数”．
（1）请写出二次函数y=2（x﹣2）2+1的“对称二次函数”；
（2）已知关于x的二次函数y1=x2﹣3x+1和y2=ax2+bx+c，若y1﹣y2与y1互为“对称二次函数”，求函数y2的表达式，并求出当﹣3≤x≤3时，y2的最大值．

【题目】为加强公路的节水意识，合理利用水资源，某市对居民用水实行阶梯水价，居民家庭每月用水量划分为两个阶梯，一、二阶梯用水的单价之比等于1：2，如图折线表示实行阶梯水价后每月水费y（元）与用水量x（m3）之间的函数关系，其中射线AB表示第二级阶梯时y与x之间的函数关系．
（1）写出点B的实际意义；
（2）求射线AB所在直线的表达式．

【题目】某中学广场上有旗杆如图1所示，在学习解直角三角形以后，数学兴趣小组测量了旗杆的长度．如图2，在某一时刻，光线与水平面的夹角为72°，旗杆AB的影子一部分落在平台上，另一部分落在斜坡上，测得落在平台上的影长BC为4米，落在斜坡上的影长CD为3米，AB⊥BC，同一时刻，若1米的竖立标杆PQ在斜坡上的影长QR为2米，求旗杆AB的长度．（结果精确到0.1米．参考数据：sin72°≈0.95，cos72°≈0.31，tan72°≈3.08）．