Question

【题目】如图1，△ABC是等腰直角三角形，四边形ADEF是正方形，D、F分别在AB、AC边上，此时BD=CF，BD⊥CF成立．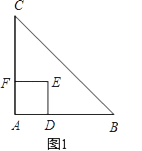
（1）当正方形ADEF绕点A逆时针旋转θ（0°＜θ＜90°）时，如图2，BD=CF成立吗？若成立，请证明；若不成立，请说明理由．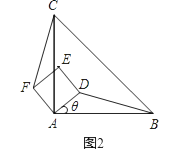
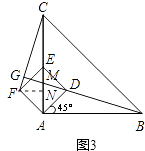
（2）当正方形ADEF绕点A逆时针旋转45°时，如图3，延长BD交CF于点G．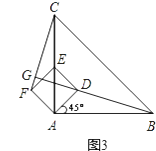
①求证：BD⊥CF；
②当AB=4，AD= 时，求线段BG的长．

Answer 1

【答案】
（1）解：BD=CF成立．

理由：∵△ABC是等腰直角三角形，四边形ADEF是正方形，

∴AB=AC，AD=AF，∠BAC=∠DAF=90°，

∵∠BAD=∠BAC﹣∠DAC，∠CAF=∠DAF﹣∠DAC，

∴∠BAD=∠CAF，

在△BAD和△CAF中，

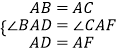
∴△BAD≌△CAF（SAS）．

∴BD=CF．

（2）①证明：设BG交AC于点M．

∵△BAD≌△CAF（已证），

∴∠ABM=∠GCM．

∵∠BMA=∠CMG，

∴△BMA∽△CMG．

∴∠BGC=∠BAC=90°．

∴BD⊥CF．

②过点F作FN⊥AC于点N．

∵在正方形ADEF中，AD=DE= ，

∴AE= =2，

∴AN=FN= AE=1．

∵在等腰直角△ABC 中，AB=4，

∴CN=AC﹣AN=3，BC= =4 ．

∴在Rt△FCN中，tan∠FCN= = ．

∴在Rt△ABM中，tan∠ABM= =tan∠FCN= ．

∴AM= AB= ．

∴CM=AC﹣AM=4﹣ = ，BM= = = ．

∵△BMA∽△CMG，

∴ ．

∴ ．

∴CG= ．

∴在Rt△BGC中，BG= = ．

【解析】（1）△ABC是等腰直角三角形，四边形ADEF是正方形，易证得△BAD≌△CAF，根据全等三角形的对应边相等，即可证得BD=CF；（2）①由△BAD≌△CAF，可得∠ABM=∠GCM，又由对顶角相等，易证得△BMA∽△CMG，根据相似三角形的对应角相等，可得BGC=∠BAC=90°，即可证得BD⊥CF；②首先过点F作FN⊥AC于点N，利用勾股定理即可求得AE，BC的长，继而求得AN，CN长，又由等角的三角函数值相等，可求得AM= AB= ，然后利用△BMA∽△CMG，求得CG的长，再由勾股定理即可求得线段BG的长．
【考点精析】认真审题，首先需要了解等腰直角三角形(等腰直角三角形是两条直角边相等的直角三角形；等腰直角三角形的两个底角相等且等于45°)，还要掌握勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2)的相关知识才是答题的关键．