
科目: 来源: 题型:
【题目】三名快递员某天的工作情况如图所示,其中点![]() ,
,![]() ,
,![]() 的横、纵坐标分别表示甲、乙、丙三名快递员上午派送快递所用的时间和件数;点
的横、纵坐标分别表示甲、乙、丙三名快递员上午派送快递所用的时间和件数;点![]() ,
,![]() ,
,![]() ,的横、纵坐标分别表示甲、乙、丙三名快递员下午派送快递所用的时间和件数.有如下三个结论:①上午派送快递所用时间最短的是甲;②下午派送快递件数最多的是丙;③在这一天中派送快递总件数最多的是乙.上述结论中,所有正确结论的序号是( )
,的横、纵坐标分别表示甲、乙、丙三名快递员下午派送快递所用的时间和件数.有如下三个结论:①上午派送快递所用时间最短的是甲;②下午派送快递件数最多的是丙;③在这一天中派送快递总件数最多的是乙.上述结论中,所有正确结论的序号是( )
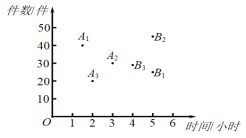
A. ①②B. ①③C. ②D. ②③
查看答案和解析>>
科目: 来源: 题型:
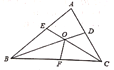
【题目】在△ABC中,已知∠A=60°,∠ABC的平分线BD与∠ACB的平分线CE相交于点O,∠BOC的平分线交BC于F,有下列结论:①∠BOE=60°,②∠ABD=∠ACE,③OE=OD,④BC=BE+CD。其中正确的是_________。(把所有正确结论的序号都选上)
查看答案和解析>>
科目: 来源: 题型:
【题目】学期即将结束,为了表彰优秀,班主任王老师用W元钱购买奖品.若以2支钢笔和3本笔记本为一份奖品,则可买60份奖品;若以2支钢笔和6本笔记本为一份奖品,则可以买40份奖品.设钢笔单价为x元/支,笔记本单价为y元/本.
(1)请用y的代数式表示x.
(2)若用这W元钱全部购买笔记本,总共可以买几本?
(3)若王老师用这W元钱恰好能买30份同样的奖品,可以选择a支钢笔和b本笔记本作为一份奖品(两种奖品都要有).请求出所有可能的a,b值.
查看答案和解析>>
科目: 来源: 题型:
【题目】利用完全平方公式因式分解在数学中的应用,请回答下列问题:
(1)因式分解:![]() ________.
________.
(2)填空:
①当![]() 时,代数式
时,代数式![]() ________;
________;
②当![]() ________时,代数式
________时,代数式![]() ;
;
③代数式![]() 的最小值是________.
的最小值是________.
(3)拓展与应用:求代数式![]() 的最小值.
的最小值.
查看答案和解析>>
科目: 来源: 题型:
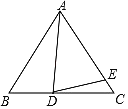
【题目】如图所示,已知在△ABC中,AB=AC,D为线段BC上一点,E为线段AC上一点,且AD=AE.
(1)若∠ABC=60°,∠ADE=70°,求∠BAD与∠CDE的度数;
(2)设∠BAD=α,∠CDE=β,试写出α、β之间的关系并加以证明.
查看答案和解析>>
科目: 来源: 题型:
【题目】若点(x1 , y1),(x2 , y2),(x3 , y3)都是反比例函数y=﹣ ![]() 图象上的点,并且y1<0<y2<y3 , 则下列各式中正确的是( )
图象上的点,并且y1<0<y2<y3 , 则下列各式中正确的是( )
A.x1<x2<x3
B.x1<x3<x2
C.x2<x1<x3
D.x2<x3<x1
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在锐角三角形ABC中,AB=4,△ABC的面积为8,BD平分∠ABC。若M、N分别是BD、BC上的动点,则CM+MN的最小值是( )
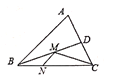
A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
科目: 来源: 题型:
【题目】求证:在直角三角形中至少有一个角不大于45°.
已知:如图所示,△ABC中,∠C=90°,求证:∠A,∠B中至少有一个不大于45°.
证明:假设__________,则∠A__________45°,∠B______45°. ∴∠A+∠B+∠C>45°+ _______+__________,这与________________________相矛盾. 所以___________不能成立,所以∠A,∠B中至少有一个角不大于45°.

查看答案和解析>>
科目: 来源: 题型:
【题目】将一副直角三角板如图放置,使GM与AB在同一直线上,其中点M在AB的中点处,MN与AC交于点E,∠BAC=30°,若AC=9cm,则EM的长为( )
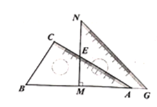
A. 2.5cm B. 3cm C. 4cm D. 4.5cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com