
科目: 来源: 题型:
【题目】已知反比例函数的图象经过点A(3,4)。
(1)这个函数的图象分布在哪些象限?y随x的增大如何变化?
(2)点B(2,6)、C( -2.5,-4.8 )和D(1,5)是否在这个函数的图象上?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知反比例函数y1=![]() 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).
的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).
(1)求这两个函数的关系式;
(2)观察图象,写出使得y1>y2成立的自变量x的取值范围;
(3)如果点C与点A关于x轴对称,求△ABC的面积.

查看答案和解析>>
科目: 来源: 题型:
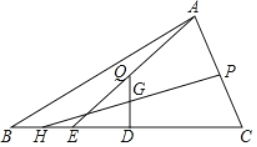
【题目】如图,在△ABC中,D为BC边中点,P为AC边中点,E为BC上一点且BE=![]() CE,连接AE,取AE中点Q并连接QD,取QD中点G,延长PG与BC边交于点H,若BC=6,则HE=_____.
CE,连接AE,取AE中点Q并连接QD,取QD中点G,延长PG与BC边交于点H,若BC=6,则HE=_____.
查看答案和解析>>
科目: 来源: 题型:
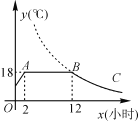
【题目】我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18 ℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=![]() 的一部分.请根据图中信息解答下列问题:
的一部分.请根据图中信息解答下列问题:
(1)恒温系统在这天保持大棚内温度18 ℃的时间有多少小时?
(2)求k的值;
(3)当x=16时,大棚内的温度约为多少度?
查看答案和解析>>
科目: 来源: 题型:
【题目】工厂加工某种茶叶,计划一周生产![]() 千克,平均每天生产
千克,平均每天生产![]() 千克,由于各种原因实际每天产量与计划量相比有出入,某周七天的生产情况记录如下(超产为正、减产为负):
千克,由于各种原因实际每天产量与计划量相比有出入,某周七天的生产情况记录如下(超产为正、减产为负):
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(![]() )这一周的实际产量是多少千克?
)这一周的实际产量是多少千克?
(![]() )该厂规定工人工资参照平均产量计发,每千克
)该厂规定工人工资参照平均产量计发,每千克![]() 元.若超产,则超产的部分每千克
元.若超产,则超产的部分每千克![]() 元;若低于平均产量,按实际产量计发,而且每少
元;若低于平均产量,按实际产量计发,而且每少![]() 千克扣除
千克扣除![]() 元,那么该工厂工人这一周的工资总额是多少?
元,那么该工厂工人这一周的工资总额是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点A(-1,3),点B(-1,-4),若常数a使得一次函数y=ax+1与线段AB有交点,且使得关于x的不等式组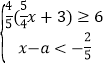 无解,则所有满足条件的整数a的个数为( )
无解,则所有满足条件的整数a的个数为( )
A. 3B. 4C. 5D. 6
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在正方形网格中,每个小正方形的边长为1,对于两个点P,Q和线段AB,给出如下定义:如果在线段AB上存在点M,N(M,N可以重合)使得PM=QN,那么称点P与点Q是线段AB的一对关联点.
(1)如图,在Q1,Q2,Q3这三个点中,与点P是线段AB的一对关联点的是 ;
(2)直线l∥线段AB,且线段AB上的任意一点到直线l的距离都是1.若点E是直线l上一动点,且点E与点P是线段AB的一对关联点,请在图中画出点E的所有位置.

查看答案和解析>>
科目: 来源: 题型:
【题目】某校科技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地.为了安全、迅速地通过这片湿地,他们沿着前进路线铺垫若干块木板,构筑成一条临时通道,从而顺利完成了任务.你能解释他们这样做的道理吗?当人和木板对湿地的压力一定时,随着木板面积S(m2)的变化,人和木板对地面的压强p(Pa)将如何变化?如果人和木板对湿地的压力合计600N,那么:
(1)用含S的代数式表示p,p是S的反比例函数吗?为什么?
(2)当木板面积为0.2m2时,压强是多少?
(3)如果要求压强不超过6000Pa,木板面积至少要多大?
查看答案和解析>>
科目: 来源: 题型:
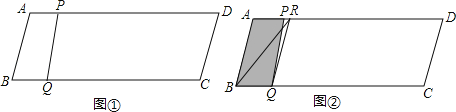
【题目】如图①,在ABCD中,AB=13,BC=50,BC边上的高为12.点P从点B出发,沿B﹣A﹣D﹣A运动,沿B﹣A运动时的速度为每秒13个单位长度,沿A﹣D﹣A运动时的速度为每秒8个单位长度.点Q从点 B出发沿BC方向运动,速度为每秒5个单位长度.P、Q两点同时出发,当点Q到达点C时,P、Q两点同时停止运动.设点P的运动时间为t(秒).连结PQ.
(1)当点P沿A﹣D﹣A运动时,求AP的长(用含t的代数式表示).
(2)连结AQ,在点P沿B﹣A﹣D运动过程中,当点P与点B、点A不重合时,记△APQ的面积为S.求S与t之间的函数关系式.
(3)过点Q作QR∥AB,交AD于点R,连结BR,如图②.在点P沿B﹣A﹣D运动过程中,当线段PQ扫过的图形(阴影部分)被线段BR分成面积相等的两部分时t的值.
(4)设点C、D关于直线PQ的对称点分别为C′、D′,直接写出C′D′∥BC时t的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司研发1000件新产品,需要精加工后才能投放市场.现在甲、乙两个工厂加工这批产品,已知甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天,而乙工厂每天加工的件数是甲工厂每天加工件数的1.25倍,公司需付甲工厂加工费用每天100元,乙工厂加工费用每天125元.
(1)甲、乙两个工厂每天各能加工多少件新产品?
(2)两个工厂同时合作完成这批产品,共付加工费多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com