
科目: 来源: 题型:
【题目】如图所示的正方形网格中,每个小正方形的边长都为1个单位长度,三角形![]() 的顶点都在正方形网格的格点上,将三角形
的顶点都在正方形网格的格点上,将三角形![]() 经过平移后得到三角形
经过平移后得到三角形![]() ,其中点
,其中点![]() 是点
是点![]() 的对应点.
的对应点.

(1)画出平移后得到的三角形![]() ;
;
(2)连接![]() 、
、![]() ,则线段
,则线段![]() 、
、![]() 的关系为______;
的关系为______;
(3)四边形![]() 的面积为______(平方单位).
的面积为______(平方单位).
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
(1)将△ABC沿x轴方向向左平移6个单位,画出平移后得到的△A1B1C1;
(2)将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2,并直接写出点B2、C2的坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠C=120°,AD=4,AB=2,点H、G分别是边CD、BC上的动点.连接AH、HG,点E为AH的中点,点F为GH的中点,连接EF则EF的最大值与最小值的差为__________.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,等腰![]() 中,
中,![]() ,
,![]() ∥
∥![]() ,CD∥
,CD∥![]() ,点
,点![]() 沿着
沿着![]() 从
从![]() 向
向![]() 运动,同时点
运动,同时点![]() 沿着
沿着![]() 从
从![]() 向
向![]() 运动,
运动,![]() 、
、![]() 两点速度相同,当
两点速度相同,当![]() 到达
到达![]() 时,两点停止运动.
时,两点停止运动.

(1)图中有__________对全等三角形.请你找一对说明理由,写出过程.
(2)在![]() 、
、![]() 运动过程中,图中阴影部分的面积是否发生变化?请说明理由.
运动过程中,图中阴影部分的面积是否发生变化?请说明理由.
(3)当![]() 平分
平分![]() 时,延长
时,延长![]() 交
交![]() 于
于![]() ,试说明
,试说明![]() .
.
(4)在(3)的条件下,若![]() ,请问此时
,请问此时![]() 点和
点和![]() 点重合吗?为什么?
点重合吗?为什么?
查看答案和解析>>
科目: 来源: 题型:
【题目】对于一个两位数,十位数字是![]() ,个位数字是
,个位数字是![]() ,总有
,总有![]() ,我们把十位上的数与个位上的数的平方和叫做这个两位数的“平方和数”,把十位上的数与个位上的数的平方差叫做“平方差数”。例如,对两位数43来说,
,我们把十位上的数与个位上的数的平方和叫做这个两位数的“平方和数”,把十位上的数与个位上的数的平方差叫做“平方差数”。例如,对两位数43来说,![]() ,
,![]() ,所以25和7分别是43的“平方和数”与“平方差数”。
,所以25和7分别是43的“平方和数”与“平方差数”。
(1)76的“平方和数”是_____________,“平万差数”是____________.
(2)5可以是___________的“平方差数”.
(3)若一个数的“平方和数”是10,“平方差数”是8,则这个数是______.
(4)若一个数的“平方和数”,与它的“平方差数”相等,那么这个数满足什么特征?为什么?(写出说明过程)
(5)若一个数的“平方差数”等子它十位上的数与个位上的数差的十倍,此时,我们把它叫做“凑整数”,请你写出两个这样的凑整数_____________,__________.
查看答案和解析>>
科目: 来源: 题型:
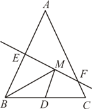
【题目】如图,等腰三角形ABC的底边BC的长为4,面积是12,腰AB的垂直平分线EF分别交AB、AC于点E、F,若点D为底边BC的中点,点M为线段EF上一动点,则△BDM的周长的最小值为_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知等腰直角![]() 和等腰直角
和等腰直角![]() 如图放置,
如图放置,![]() ,
,![]() ,
,![]() ,其中,
,其中,![]() 、
、![]() 、
、![]() 在一条直线上,连接
在一条直线上,连接![]() 并延长交
并延长交![]() 于
于![]() ,
,

(1)求证:![]()
(2)![]() 与
与![]() 有什么位置关系?请说明理由.
有什么位置关系?请说明理由.
(3)若![]() ,
,![]() 与
与![]() 有什么数量关系?请说明理由.
有什么数量关系?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】小东家与学校之间是一条笔直的公路,早饭后,小东歩行前往学校,途中发现忘带画板,停下给妈妈打电话,妈妈接到电话后,带上画板马上赶往学校,同时小东沿原路返回,两人相遇后,小东立即赶往学校,妈妈沿原路返回,![]() 时到家,假设小东始终以
时到家,假设小东始终以![]() 的速度步行,两人离家的距离
的速度步行,两人离家的距离![]() (单位:
(单位:![]() )与小东打完电话后的步行时间
)与小东打完电话后的步行时间![]() (单位:
(单位:![]() )之间的函数关系如图所示:
)之间的函数关系如图所示:

(1)小东打电话时,他离家__________![]() .
.
(2)在图中的空格中,填上相应的数据.
(3)小东和妈妈相遇后,妈妈回家的速度为_________![]() .
.
(4)_____________ ![]() 时,两人相距
时,两人相距![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】推理填空
已知,如图,![]() ∥
∥![]() ,
,![]() ∥
∥![]() ,
,![]() 平分
平分![]() 交
交![]() 于
于![]() ,
,![]() 平分
平分![]() 交
交![]() 于
于![]() ,求证:
,求证:![]() ∥
∥![]()

证明:∵![]() ∥
∥![]()
∴![]() __________
__________![]() (两直线平行,同旁内角互补)
(两直线平行,同旁内角互补)
∵![]() ∥
∥![]()
∴![]() __________
__________![]() (两直线平行,同旁内角互补)
(两直线平行,同旁内角互补)
∴_____________=________________
又∵![]() 平分
平分![]()
∴____________![]() (角平分线定义)
(角平分线定义)
又∵![]() 平分
平分![]()
∴____________![]() (角平分线定义)
(角平分线定义)
∴_____________=________________
∵![]() ∥
∥![]()
∴![]() ___________(两直线平行,内错角相等)
___________(两直线平行,内错角相等)
∴_____________=________________(等量代换)
∴![]() ∥
∥![]() (同位角相等,两直线平行)
(同位角相等,两直线平行)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com