
科目: 来源: 题型:
【题目】某校想了解学生每周的课外阅读时间情况,随机调查了部分学生,对学生每周的课外阅读时间x(单位:小时)进行分组整理,并绘制了如图所示的不完整的频数分别直方图和扇形统计图:

根据图中提供的信息,解答下列问题:
(1)补全频数分布直方图
(2)求扇形统计图中m的值和E组对应的圆心角度数
(3)请估计该校3000名学生中每周的课外阅读时间不小于6小时的人数
查看答案和解析>>
科目: 来源: 题型:
【题目】(2014贵州黔东南)黔东南州某超市计划购进一批甲、乙两种玩具,已知5件甲种玩具的进价与3件乙种玩具的进价的和为231元,2件甲种玩具的进价与3件乙种玩具的进价的和为141元.
(1)求每件甲种、乙种玩具的进价分别是多少元;
(2)如果购进甲种玩具有优惠,优惠方法是:购进甲种玩具超过20件,超出部分可以享受7折优惠.若购进x(x>0)件甲种玩具需要花费y元,请你求出y与x的函数关系式;
(3)在(2)的条件下,超市决定在甲、乙两种玩具中选购其中一种,且数量超过20件,请你帮助超市判断购进哪种玩具省钱.
查看答案和解析>>
科目: 来源: 题型:
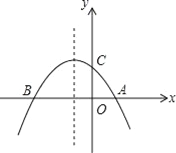
【题目】如图,已知抛物线y=﹣![]() x2﹣
x2﹣![]() x+2与x轴交于A、B两点,与y轴交于点C
x+2与x轴交于A、B两点,与y轴交于点C
(1)求点A,B,C的坐标;
(2)点E是此抛物线上的点,点F是其对称轴上的点,求以A,B,E,F为顶点的平行四边形的面积;
(3)此抛物线的对称轴上是否存在点M,使得△ACM是等腰三角形?若存在,请求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
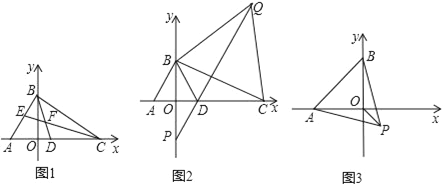
【题目】如图,在平面直角坐标系中,A(﹣3,0),点 B是 y轴正半轴上一动点,点C、D在 x正半轴上.
(1)如图,若∠BAO=60°,∠BCO=40°,BD、CE 是△ABC的两条角平分线,且BD、CE交于点F,直接写出CF的长_____.
(2)如图,△ABD是等边三角形,以线段BC为边在第一象限内作等边△BCQ,连接 QD并延长,交 y轴于点 P,当点 C运动到什么位置时,满足 PD=![]() DC?请求出点C的坐标;
DC?请求出点C的坐标;
(3)如图,以AB为边在AB的下方作等边△ABP,点B在 y轴上运动时,求OP的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图点 P 是等边△ABC 内一点,将△APC 绕点 C 顺时针旋转 60°得到△BDC,连接 PD.
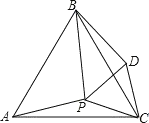
(1)求证:△DPC 是等边三角形;
(2)当∠APC=150°时,试判断△DPB 的形状,并说明理由;
(3)当∠APB=100°且△DPB 是等腰三角形,求∠APC 的度数。
查看答案和解析>>
科目: 来源: 题型:
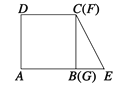
【题目】如图,将边长为 ![]() 的正方形
的正方形 ![]() 的一边
的一边 ![]() 与直角边分别是
与直角边分别是 ![]() 和
和 ![]() 的
的 ![]() 的一边
的一边 ![]() 重合.正方形
重合.正方形 ![]() 以每秒
以每秒 ![]() 个单位长度的速度沿
个单位长度的速度沿 ![]() 向右匀速运动,当点
向右匀速运动,当点 ![]() 和点
和点 ![]() 重合时正方形停止运动.设正方形的运动时间为
重合时正方形停止运动.设正方形的运动时间为 ![]() 秒,正方形
秒,正方形 ![]() 与
与 ![]() 重叠部分面积为S,则S关于
重叠部分面积为S,则S关于 ![]() 的函数图象为( )
的函数图象为( )
A. 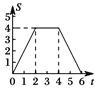 B.
B. 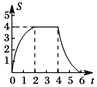 C.
C.  D.
D. 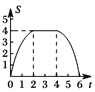
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知∠BAE+∠AED=180°,∠1=∠2,那么∠F=∠G吗?为什么?
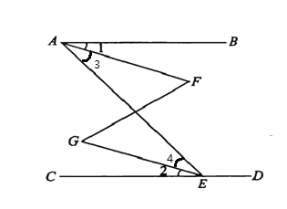
解:因为∠BAE+∠AED=180°( 已知)
所以AB∥CD________
所以∠BAE=∠AEC________
因为∠1=∠2( 已知)
所以∠BAE—∠1=∠AEC—∠2(等式性质)
即∠3=∠4
所以AF∥EG________,
所以∠F=∠G________.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:![]() ,OB、OM、ON,是
,OB、OM、ON,是![]() 内的射线.
内的射线.
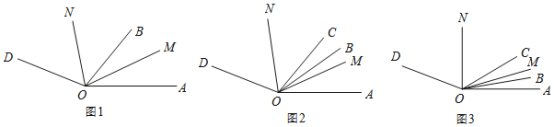
(1)如图 1,若 OM 平分 ![]() , ON平分
, ON平分![]() .当射线OB 绕点O 在
.当射线OB 绕点O 在![]() 内旋转时,
内旋转时,![]() = 度.
= 度.
(2)OC也是![]() 内的射线,如图2,若
内的射线,如图2,若![]() ,OM平分
,OM平分![]() ,ON平分
,ON平分![]() ,当射线OB绕点O在
,当射线OB绕点O在![]() 内旋转时,求
内旋转时,求![]() 的大小.
的大小.
(3)在(2)的条件下,当射线OB从边OA开始绕O点以每秒![]() 的速度逆时针旋转t秒,如图3,若
的速度逆时针旋转t秒,如图3,若![]() ,求t的值.
,求t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com