【题目】在
中，边
的垂直平分线分别交
于点
，若
，则
的度数为_________．
【答案】65°或115°．
【解析】
根据线段的垂直平分线的性质得到DA＝DB，EA＝EC，根据等腰三角形的性质得到∠DAB＝∠B，∠EAC＝∠C，根据三角形内角和定理计算即可．
解：如图1，∵DM，EN分别垂直平分AB和AC，
∴DA＝DB，EA＝EC，
∴∠DAB＝∠B，∠EAC＝∠C，
∠DAB＋∠B＋∠EAC＋∠C∠DAE＝180°，
则2（∠B＋∠C）＝230°，
解得，∠B＋∠C＝115°，
∴∠BAC＝65°，
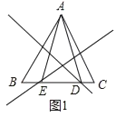
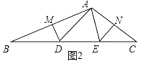
如图2
∵DM，EN分别垂直平分AB和AC，
∴DA＝DB，EA＝EC，
∴∠DAB＝∠B，∠EAC＝∠C，
∠DAB＋∠B＋∠EAC＋∠C＋∠DAE＝180°，
则2（∠B＋∠C）＝130°，
解得，∠B＋∠C＝65°，
∴∠BAC＝115°，
故答案为：65°或115°．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
【题目】如图，正方形ABCD由四个相同的大长方形，四个相同的小长形以及一个小正方形组成，其中四个大长方形的长和宽分别是小长方形长和宽的2倍，若中间小正方形的面积为1，则大正方形ABCD的面积是（ ）
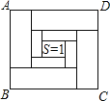
A.36B.25C.20D.16
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB=AC，AB的垂直平分线交AB于M，交AC于N．
（1）若∠ABC=70°，则∠MNA的度数是__．
（2）连接NB，若AB=8cm，△NBC的周长是14cm．
①求BC的长；
②在直线MN上是否存在P，使由P、B、C构成的△PBC的周长值最小？若存在，标出点P的位置并求△PBC的周长最小值；若不存在，说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知∠BAE＋∠AED＝180°，∠1＝∠2，那么∠F＝∠G吗？为什么？
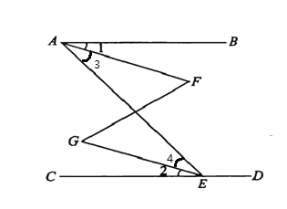
解：因为∠BAE＋∠AED＝180°( 已知)
所以AB∥CD________
所以∠BAE＝∠AEC________
因为∠1＝∠2( 已知)
所以∠BAE—∠1＝∠AEC—∠2(等式性质)
即∠3＝∠4
所以AF∥EG________，
所以∠F＝∠G________.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某中学九年级的同学参加了一项“节能环保”的社会调查活动，为了了解家庭用电的情况，他们随机调查了某城区50 个家庭一年中生活用电的电费支出情况，并绘制了如下不完整的频数分布表和频数分布直方图（费用取整数，单位：元）．
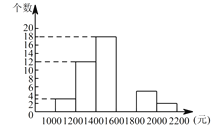
请你根据以上提供的信息，解答下列问题：
（1）频数分布表中 
________________，
________________，
（2）补全频数分布直方图；
（3）这 
个家庭电费支出的中位数落在________组内；
（4）若该城区有 
万个家庭，请你估计该城区有多少个一年电费支出低于 
元的家庭?
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，正方形ABCD的对角线交于点O，以AD为边向外作Rt△ADE，∠AED=90°，连接OE，DE=6，OE=8
，则另一直角边AE的长为_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读理解：在平面直角坐标系中，若两点P、Q的坐标分别是P（x1，y1）、
Q（x2，y2），则P、Q这两点间的距离为|PQ|=
．如P（1，2），Q（3，4），则|PQ|=
=2
．
对于某种几何图形给出如下定义：符合一定条件的动点形成的图形，叫做符合这个条件的点的轨迹．如平面内到线段两个端点距离相等的点的轨迹是这条线段的垂直平分线．
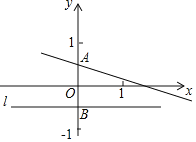
解决问题：如图，已知在平面直角坐标系xOy中，直线y=kx+
交y轴于点A，点A关于x轴的对称点为点B，过点B作直线l平行于x轴．
（1）到点A的距离等于线段AB长度的点的轨迹是 ；
（2）若动点C（x，y）满足到直线l的距离等于线段CA的长度，求动点C轨迹的函数表达式；
问题拓展：（3）若（2）中的动点C的轨迹与直线y=kx+交于E、F两点，分别过E、F作直线l的垂线，垂足分别是M、N，求证：①EF是△AMN外接圆的切线；②
为定值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
