
【题目】阅读理解:在平面直角坐标系中,若两点P、Q的坐标分别是P(x1,y1)、
Q(x2,y2),则P、Q这两点间的距离为|PQ|=![]() .如P(1,2),Q(3,4),则|PQ|=
.如P(1,2),Q(3,4),则|PQ|=![]() =2
=2![]() .
.
对于某种几何图形给出如下定义:符合一定条件的动点形成的图形,叫做符合这个条件的点的轨迹.如平面内到线段两个端点距离相等的点的轨迹是这条线段的垂直平分线.
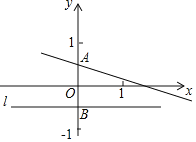
解决问题:如图,已知在平面直角坐标系xOy中,直线y=kx+![]() 交y轴于点A,点A关于x轴的对称点为点B,过点B作直线l平行于x轴.
交y轴于点A,点A关于x轴的对称点为点B,过点B作直线l平行于x轴.
(1)到点A的距离等于线段AB长度的点的轨迹是 ;
(2)若动点C(x,y)满足到直线l的距离等于线段CA的长度,求动点C轨迹的函数表达式;
问题拓展:(3)若(2)中的动点C的轨迹与直线y=kx+![]() 交于E、F两点,分别过E、F作直线l的垂线,垂足分别是M、N,求证:①EF是△AMN外接圆的切线;②
交于E、F两点,分别过E、F作直线l的垂线,垂足分别是M、N,求证:①EF是△AMN外接圆的切线;②![]() 为定值.
为定值.
【答案】(1)x2+(y﹣![]() )2=1;(2)动点C轨迹的函数表达式y=
)2=1;(2)动点C轨迹的函数表达式y=![]() x2;(3)①证明见解析;②证明见解析.
x2;(3)①证明见解析;②证明见解析.
【解析】
(1)利用两点间的距离公式即可得出结论;
(2)利用两点间的距离公式即可得出结论;
(3)①先确定出m+n=2k,mn=﹣1,再确定出M(m,﹣![]() ),N(n,﹣
),N(n,﹣![]() ),进而判断出△AMN是直角三角形,再求出直线AQ的解析式为y=﹣
),进而判断出△AMN是直角三角形,再求出直线AQ的解析式为y=﹣![]() x+
x+![]() ,即可得出结论;
,即可得出结论;
②先确定出a=mk+![]() ,b=nk+
,b=nk+![]() ,再求出AE=ME=a+
,再求出AE=ME=a+![]() =mk+1,AF=NF=b+
=mk+1,AF=NF=b+![]() =nk+1,即可得出结论.
=nk+1,即可得出结论.
(1)设到点A的距离等于线段AB长度的点D坐标为(x,y),
∴AD2=x2+(y﹣![]() )2,
)2,
∵直线y=kx+![]() 交y轴于点A,
交y轴于点A,
∴A(0,![]() ),
),
∵点A关于x轴的对称点为点B,
∴B(0,﹣![]() ),
),
∴AB=1,
∵点D到点A的距离等于线段AB长度,
∴x2+(y﹣![]() )2=1,
)2=1,
故答案为:x2+(y﹣![]() )2=1;
)2=1;
(2)∵过点B作直线l平行于x轴,
∴直线l的解析式为y=﹣![]() ,
,
∵C(x,y),A(0,![]() ),
),
∴AC2=x2+(y﹣![]() )2,点C到直线l的距离为:(y+
)2,点C到直线l的距离为:(y+![]() ),
),
∵动点C(x,y)满足到直线l的距离等于线段CA的长度,
∴x2+(y﹣![]() )2=(y+
)2=(y+![]() )2,
)2,
∴动点C轨迹的函数表达式y=![]() x2;
x2;
(3)①如图,
设点E(m,a)点F(n,b),
∵动点C的轨迹与直线y=kx+![]() 交于E、F两点,
交于E、F两点,
∴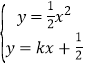 ,
,
∴x2﹣2kx﹣1=0,
∴m+n=2k,mn=﹣1,
∵过E、F作直线l的垂线,垂足分别是M、N,
∴M(m,﹣![]() ),N(n,﹣
),N(n,﹣![]() ),
),
∵A(0,![]() ),
),
∴AM2+AN2=m2+1+n2+1=m2+n2+2=(m+n)2﹣2mn+2=4k2+4,
MN2=(m﹣n)2=(m+n)2﹣4mn=4k2+4,
∴AM2+AN2=MN2,
∴△AMN是直角三角形,MN为斜边,
取MN的中点Q,
∴点Q是△AMN的外接圆的圆心,
∴Q(k,﹣![]() ),
),
∵A(0,![]() ),
),
∴直线AQ的解析式为y=﹣![]() x+
x+![]() ,
,
∵直线EF的解析式为y=kx+![]() ,
,
∴AQ⊥EF,
∴EF是△AMN外接圆的切线;
②∵点E(m,a)点F(n,b)在直线y=kx+![]() 上,
上,
∴a=mk+![]() ,b=nk+
,b=nk+![]() ,
,
∵ME,NF,EF是△AMN的外接圆的切线,
∴AE=ME=a+![]() =mk+1,AF=NF=b+
=mk+1,AF=NF=b+![]() =nk+1,
=nk+1,
∴![]() =
=![]() =2,
=2,
即:![]() 为定值,定值为2.
为定值,定值为2.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B>90°,CD为∠ACB的角平分线,在AC边上取点E,使DE=DB,且∠AED>90°.若∠A=α,∠ACB=β,则( )
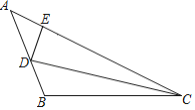
A.∠AED=180°﹣α﹣βB.∠AED=180°﹣α﹣![]() β
β
C.∠AED=90°﹣α+βD.∠AED=90°+α+![]() β
β
查看答案和解析>>
科目:初中数学 来源: 题型:
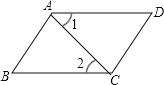
【题目】 根据题意,完成推理填空:如图,AB∥CD,∠1=∠2,试说明∠B=∠D.
解:∵∠1=∠2(已知)
∴ (內错角相等,两直线平行)
∴∠BAD+∠B=180°(两直线平行,同旁内角互补)
∵AB∥CD
∴ + =180°,
∴∠B=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() ,其中
,其中![]() .
.
(1)若点![]() 在y1的图象上.求a的值:
在y1的图象上.求a的值:
(2)当![]() 时.若函数有最大值2.求y1的函数表达式;
时.若函数有最大值2.求y1的函数表达式;
(3)对于一次函数![]() ,其中
,其中![]() ,若对- -切实数x,
,若对- -切实数x,![]() 都成立,求a,m需满足的数量关系及 a的取值范围.
都成立,求a,m需满足的数量关系及 a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017湖南株洲)如图示,若△ABC内一点P满足∠PAC=∠PBA=∠PCB,则点P为△ABC的布洛卡点.三角形的布洛卡点(Brocard point)是法国数学家和数学教育家克洛尔(A.L.Crelle 1780﹣1855)于1816年首次发现,但他的发现并未被当时的人们所注意,1875年,布洛卡点被一个数学爱好者法国军官布洛卡(Brocard 1845﹣1922)重新发现,并用他的名字命名.问题:已知在等腰直角三角形DEF中,∠EDF=90°,若点Q为△DEF的布洛卡点,DQ=1,则EQ+FQ=( )
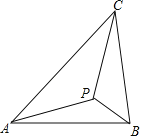
A. 5 B. 4 C. 3+![]() D. 2+
D. 2+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
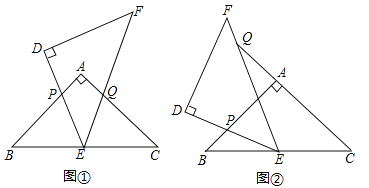
【题目】(2017甘肃省天水市)△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合,将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q.
(1)如图①,当点Q在线段AC上,且AP=AQ时,求证:△BPE≌△CQE;
(2)如图②,当点Q在线段CA的延长线上时,求证:△BPE∽△CEQ;并求当BP=2,CQ=9时BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为平行四边形纸片.把纸片ABCD折叠,使点B恰好落在CD边上,折痕为AF.且AB=10cm、AD=8cm、DE=6cm.
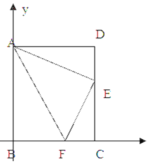
(1)求证:平行四边形ABCD是矩形;
(2)如图2,以点B为坐标原点,水平方向、竖直方向为x轴、y轴建立平面直角坐标系,求直线AF的解析式;
(3)在(2)中的坐标系内是否存在这样的点P,使得以点P、A、E、F为顶点的四边形是平行四边形?若不存在,请说明理由;若存在,直接写出点P的坐标。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com