
【题目】已知一次函数![]() ,其中
,其中![]() .
.
(1)若点![]() 在y1的图象上.求a的值:
在y1的图象上.求a的值:
(2)当![]() 时.若函数有最大值2.求y1的函数表达式;
时.若函数有最大值2.求y1的函数表达式;
(3)对于一次函数![]() ,其中
,其中![]() ,若对- -切实数x,
,若对- -切实数x,![]() 都成立,求a,m需满足的数量关系及 a的取值范围.
都成立,求a,m需满足的数量关系及 a的取值范围.
【答案】(1) ![]() ;(2)
;(2) ![]() 或
或![]() ;(3)
;(3)![]() 且
且![]() 且
且![]() .
.
【解析】
(1) 把![]() 代入
代入![]() 中可求出a的值;
中可求出a的值;
(2)讨论:当![]() , 即a> 1时,根据一次函数的性质得到x=3时,y=2,然后把(3,2)代入
, 即a> 1时,根据一次函数的性质得到x=3时,y=2,然后把(3,2)代入![]() 中求Ha得到此时一次函数解析式;当a-1<0, 即a<1时,利用一次函数的性质得到x=-2时,y=2,然后把(-2,2) 代入
中求Ha得到此时一次函数解析式;当a-1<0, 即a<1时,利用一次函数的性质得到x=-2时,y=2,然后把(-2,2) 代入![]() 中求出a得到此时一次函数解析式;
中求出a得到此时一次函数解析式;
(3)先整理得到![]() ,再对一切实数x,
,再对一切实数x,![]() 都成立,则直线y与y平行,且y在y的上方,所以
都成立,则直线y与y平行,且y在y的上方,所以![]() 且
且![]() ,从而得到a,m需满足的数量关系及a的取值范围.
,从而得到a,m需满足的数量关系及a的取值范围.
(1) 把![]() 代入
代入![]() 得
得![]() ,
,
![]() ;
;
(2)当a-1>0,即a> 1时,则x=3时,y=2,
把(3,2)代入![]() 得
得![]() ,解得a=4,此时一次函数解析式为
,解得a=4,此时一次函数解析式为![]() ;
;
当a-1<0,即a<1时,则x=-2时,y=2,
把(-2,2)代入![]() 得
得![]() ,解得
,解得![]() ,此时一.次函数解析式为
,此时一.次函数解析式为![]() ;
;
(3)![]() ,
,
∵对一切实数x,![]() 都成立,
都成立,
![]() 且
且![]() ,
,
![]() 且
且![]() 且
且![]()


科目:初中数学 来源: 题型:
【题目】某中学九年级的同学参加了一项“节能环保”的社会调查活动,为了了解家庭用电的情况,他们随机调查了某城区50 个家庭一年中生活用电的电费支出情况,并绘制了如下不完整的频数分布表和频数分布直方图(费用取整数,单位:元).

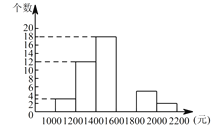
请你根据以上提供的信息,解答下列问题:
(1)频数分布表中 ![]() ________________,
________________,![]() ________________,
________________,
(2)补全频数分布直方图;
(3)这 ![]() 个家庭电费支出的中位数落在________组内;
个家庭电费支出的中位数落在________组内;
(4)若该城区有 ![]() 万个家庭,请你估计该城区有多少个一年电费支出低于
万个家庭,请你估计该城区有多少个一年电费支出低于 ![]() 元的家庭?
元的家庭?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】荆州市滨江公园旁的万寿宝塔始建于明嘉靖年间,周边风景秀丽.现在塔底低于地面约7米,某校学生测得古塔的整体高度约为40米.其测量塔顶相对地面高度的过程如下:先在地面A处测得塔顶的仰角为30°,再向古塔方向行进a米后到达B处,在B处测得塔顶的仰角为45°(如图所示),那么a的值约为_____米(![]() ≈1.73,结果精确到0.1).
≈1.73,结果精确到0.1).
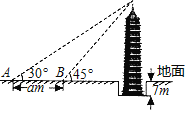
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】速度分别为100km/h和akm/h(0<a<100)的两车分别从相距s千米的两地同时出发,沿同一方向匀速前行.行驶一段时间后,其中一车按原速度原路返回,直到与另一车相遇时两车停止.在此过程中,两车之间的距离y(km)与行驶时间t(h)之间的函数关系如图所示.下列说法:①a=60;②b=2;③c=b+![]() ;④若s=60,则b=
;④若s=60,则b=![]() .其中说法正确的是( )
.其中说法正确的是( )

A.①②③B.②③④C.①②④D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:在平面直角坐标系中,若两点P、Q的坐标分别是P(x1,y1)、
Q(x2,y2),则P、Q这两点间的距离为|PQ|=![]() .如P(1,2),Q(3,4),则|PQ|=
.如P(1,2),Q(3,4),则|PQ|=![]() =2
=2![]() .
.
对于某种几何图形给出如下定义:符合一定条件的动点形成的图形,叫做符合这个条件的点的轨迹.如平面内到线段两个端点距离相等的点的轨迹是这条线段的垂直平分线.
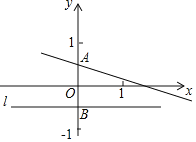
解决问题:如图,已知在平面直角坐标系xOy中,直线y=kx+![]() 交y轴于点A,点A关于x轴的对称点为点B,过点B作直线l平行于x轴.
交y轴于点A,点A关于x轴的对称点为点B,过点B作直线l平行于x轴.
(1)到点A的距离等于线段AB长度的点的轨迹是 ;
(2)若动点C(x,y)满足到直线l的距离等于线段CA的长度,求动点C轨迹的函数表达式;
问题拓展:(3)若(2)中的动点C的轨迹与直线y=kx+![]() 交于E、F两点,分别过E、F作直线l的垂线,垂足分别是M、N,求证:①EF是△AMN外接圆的切线;②
交于E、F两点,分别过E、F作直线l的垂线,垂足分别是M、N,求证:①EF是△AMN外接圆的切线;②![]() 为定值.
为定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某烤鸭店在确定烤鸭的烤制时间时,主要依据的是下表的数据:
鸭的质量/千克 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
烤制时间/分 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 |
设鸭的质量为![]() 千克,烤制时间为
千克,烤制时间为![]() ,估计当
,估计当![]() 千克时,
千克时,![]() 的值为( )
的值为( )
A.138B.140C.148D.160
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证:△ADE∽△ABC;
(2)若AD=3,AB=5,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
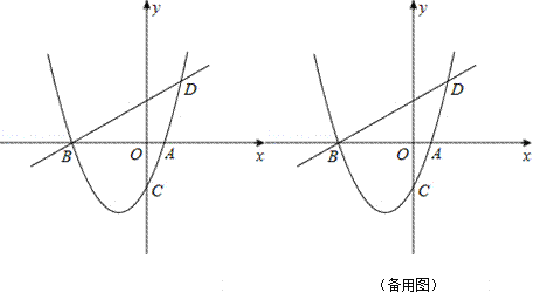
【题目】如图,已知抛物线y=ax2+bx﹣2(a≠0)与x轴交于A、B两点,与y轴交于C点,直线BD交抛物线于点D,并且D(2,3),tan∠DBA=![]() .
.
(1)求抛物线的解析式;
(2)已知点M为抛物线上一动点,且在第三象限,顺次连接点B、M、C、A,求四边形BMCA面积的最大值;
(3)在(2)中四边形BMCA面积最大的条件下,过点M作直线平行于y轴,在这条直线上是否存在一个以Q点为圆心,OQ为半径且与直线AC相切的圆?若存在,求出圆心Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
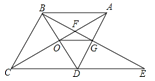
【题目】如图,在菱形ABCD中,∠BAD=60°,AC与BD交于点O,E为CD延长线上的一点,且CD=DE,连接BE分别交AC、AD于点F、G,连接OG,则下列结论中一定成立的是( )
①OG=![]() AB;②与△EGD全等的三角形共有5个;③S四边形ODGF>S△ABF;④由点A、B、D、E构成的四边形是菱形.
AB;②与△EGD全等的三角形共有5个;③S四边形ODGF>S△ABF;④由点A、B、D、E构成的四边形是菱形.
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com