
科目: 来源: 题型:
【题目】如图,直线l1:y1=-![]() x+m与y轴交于点A(0,6),直线l2:y2=kx+1分别与x轴交于点B(-2,0),与y轴交于点C,两条直线l1、l2相交于点D,连接AB.
x+m与y轴交于点A(0,6),直线l2:y2=kx+1分别与x轴交于点B(-2,0),与y轴交于点C,两条直线l1、l2相交于点D,连接AB.
(1)求两直线l1、l2交点D的坐标;
(2)求△ABD的面积.

查看答案和解析>>
科目: 来源: 题型:
【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.

(1)根据图示填写下表;
平均数(分) | 中位数(分) | 众数(分) | |
初中部 | 85 | ||
高中部 | 85 | 100 |
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
查看答案和解析>>
科目: 来源: 题型:
【题目】某水果经销商上月份销售一种新上市的水果,平均售价为10元/千克,月销售量为1000千克.经市场调查,若将该种水果价格调低至x元/千克,则本月份销售量y(千克)与x(元/千克)之间符合一次函数关系,并且得到了表中的数据:
价格x(元/千克) | 7 | 5 |
价格y(千克) | 2000 | 4000 |
(1)求y与x之间的函数解析式;
(2)已知该种水果上月份的成本价为5元/千克,本月份的成本价为4元/千克,要使本月份销售该种水果所获利润比上月份增加20%,同时又要让顾客得到实惠,那么该种水果价格每千克应调低至多少元?
查看答案和解析>>
科目: 来源: 题型:
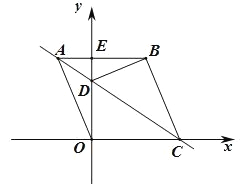
【题目】如图,四边形 ABCO 是菱形,以点 O 为坐标原点,OC 所在直线为![]() 轴建立平面直角坐标系.若点 A 的坐 标为(-5,12),直线 AC、边 AB 与
轴建立平面直角坐标系.若点 A 的坐 标为(-5,12),直线 AC、边 AB 与![]() 轴的交点分别是点 D 与点 E,连接 BD.
轴的交点分别是点 D 与点 E,连接 BD.
(1)求菱形 ABCO 的边长;
(2)求 BD 所在直线的解析式;
(3)直线 AC 上是否存在一点 P 使得![]() 与
与![]() 的面积相等?若存在,请直接写出点 P 的坐标;若不存在,请说明理由.
的面积相等?若存在,请直接写出点 P 的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
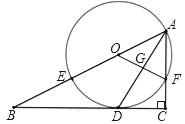
【题目】如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,O为AB上一点,经过点A,D的⊙O分别交AB,AC于点E,F,连接OF交AD于点G.
(1)求证:BC是⊙O的切线;
(2)设AB=x,AF=y,试用含x,y的代数式表示线段AD的长;
(3)若BE=8,sinB=![]() ,求DG的长,
,求DG的长,
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,边长为1的正方形ABCD中,AC 、DB交于点H.DE平分∠ADB,交AC于点E.联结BE并延长,交边AD于点F.
(1)求证:DC=EC;
(2)求△EAF的面积.

![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读材料:求解一元一次方程,需要根据等式的基本性质,把方程转化为x=a的形式;求解二元一次方程组,需要通过消元把它转化为一元一次方程来解;求解三元一次方程组,需要把它转化为二元一次方程组来解;求解一元二次方程,需要把它转化为两个一元一次方程来解;求解分式方程,需要通过去分母把它转化为整式方程来解,各类方程的解法不尽相同,但是它们都用到一种共同的基本数学思想﹣转化,即把未知转化为已知来求解.
用“转化“的数学思想,我们还可以解一些新的方程.
例如,解一元三次方程x3+x2﹣2x=0,通过因式分解把它转化为x(x2+x﹣2)=0,通过解方程x=0和x2+x﹣2=0,可得原方程x3+x2﹣2x=0的解.
再例如,解根号下含有来知数的方程:![]() =x,通过两边同时平方把它转化为2x+3=x2,解得:x1=3,x2=﹣1.因为2x+3≥0,且x≥0,所以x=﹣1不是原方程的根,x=3是原方程的解.
=x,通过两边同时平方把它转化为2x+3=x2,解得:x1=3,x2=﹣1.因为2x+3≥0,且x≥0,所以x=﹣1不是原方程的根,x=3是原方程的解.
(1)问题:方程x3+x2﹣2x=0的解是x1=0,x2= ,x3= .
(2)拓展:求方程![]() =x﹣1的解;
=x﹣1的解;
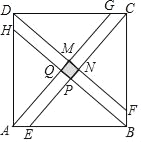
(3)应用:在一个边长为1的正方形中构造一个如图所示的正方形;在正方形ABCD边上依次截取AE=BF=CG=DH=![]() ,连接AG,BH,CE,DF,得到正方形MNPQ,若小正方形MNPQ(图中阴影部分)的边长为
,连接AG,BH,CE,DF,得到正方形MNPQ,若小正方形MNPQ(图中阴影部分)的边长为![]() ,求n的值.
,求n的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某店只销售某种进价为40元/kg的产品,已知该店按60元kg出售时,每天可售出100kg,后来经过市场调查发现,单价每降低1元,则每天的销售量可增加10kg.
(1)若单价降低2元,则每天的销售量是_____千克,每天的利润为_____元;若单价降低x元,则每天的销售量是_____千克,每天的利润为______元;(用含x的代数式表示)
(2)若该店销售这种产品计划每天获利2240元,单价应降价多少元?
(3)当单价降低多少元时,该店每天的利润最大,最大利润是多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线y=ax2﹣ax﹣2a(a为常数且不等于0)与x轴的交点为A,B两点,且A点在B的右侧.
(1)当抛物线经过点(3,8),求a的值;
(2)求A、B两点的坐标;
(3)若抛物线的顶点为M,且点M到x轴的距离等于AB的3倍,求抛物线的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com