
科目: 来源: 题型:
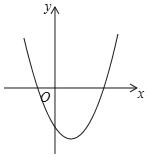
【题目】如图,在平直角坐标系中,O为坐标原点,抛物线y=x2﹣mx﹣1的对称轴为直线x=1.若关于x的一元二次方程x2﹣mx﹣1﹣n=0(n为实数)在0<x<3的范围内有解,则n的取值范围是______.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点A在函数y=![]() (x>0)的图象上,过点A作x轴、y轴的垂线分别交函数y=
(x>0)的图象上,过点A作x轴、y轴的垂线分别交函数y=![]() (x>0,k>2)的图象于点B、C,过点C作x轴的垂线交y=
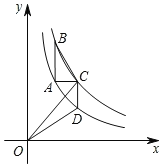
(x>0,k>2)的图象于点B、C,过点C作x轴的垂线交y=![]() (x>0)的图象于点D,连结BC、OC、OD.若点A、C的横坐标分别为1和2,则△ABC与△OCD的面积之和为( )
(x>0)的图象于点D,连结BC、OC、OD.若点A、C的横坐标分别为1和2,则△ABC与△OCD的面积之和为( )
A.2B.3C.4D.6
查看答案和解析>>
科目: 来源: 题型:
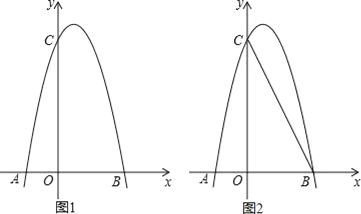
【题目】如图1,对称轴为直线x=![]() 的抛物线经过B(2,0)、C(0,4)两点,抛物线与x轴的另一交点为A
的抛物线经过B(2,0)、C(0,4)两点,抛物线与x轴的另一交点为A
(1)求抛物线的解析式;
(2)若点P为第一象限内抛物线上的一点,设四边形COBP的面积为S,求S的最大值;
(3)如图2,若M是线段BC上一动点,在x轴是否存在这样的点Q,使△MQC为等腰三角形且△MQB为直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
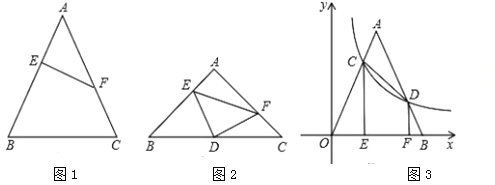
【题目】如图1,等腰![]() 中,点
中,点![]() 分别在腰
分别在腰![]() 上,连结
上,连结![]() ,若
,若![]() ,则称
,则称![]() 为该等腰三角形的逆等线.
为该等腰三角形的逆等线.
(1)如图1,![]() 是等腰
是等腰![]() 的逆等线,若
的逆等线,若![]() ,求逆等线
,求逆等线![]() 的长;
的长;
(2)如图2,若直角![]() 的直角顶点
的直角顶点![]() 恰好为等腰直角
恰好为等腰直角![]() 底边
底边![]() 上的中点,且点
上的中点,且点![]() 分别在
分别在![]() 上,求证:
上,求证:![]() 为等腰
为等腰![]() 的逆等线;
的逆等线;
(3)如图3,等腰![]() 的顶点
的顶点![]() 与原点重合,底边
与原点重合,底边![]() 在
在![]() 轴上,反比例函数
轴上,反比例函数![]() 的图象交
的图象交![]() 于点
于点![]() ,若
,若![]() 恰为
恰为![]() 的逆等线,过点
的逆等线,过点![]() 分别作
分别作![]() 轴于点
轴于点![]() 轴于点
轴于点![]() ,已知
,已知![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
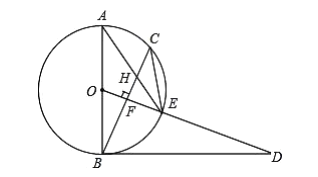
【题目】已知,如图,![]() 是⊙
是⊙![]() 的直径,点
的直径,点![]() 为⊙
为⊙![]() 上一点,
上一点,![]() 于点
于点![]() ,交⊙
,交⊙![]() 于点
于点![]() 与
与![]() 交于点
交于点![]() ,点
,点![]() 为
为![]() 的延长线上一点,且
的延长线上一点,且![]() .
.
(1)试判断直线![]() 与⊙
与⊙![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若⊙![]() 的半径为
的半径为![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
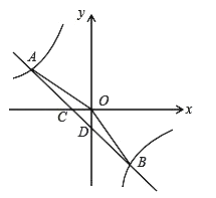
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于第二、四象限内的
的图象交于第二、四象限内的![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 的坐标是
的坐标是![]() ,连接
,连接![]() ,且
,且![]() .
.
(1)求这个反比例函数和一次函数的解析式;
(2)根据图象,直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目: 来源: 题型:
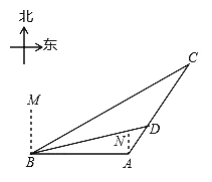
【题目】今年,我国海关总署严厉打击“洋垃圾”违法行动,坚决把“洋垃圾”拒于国门之外如图,某天我国一艘海监船巡航到![]() 港口正西方的
港口正西方的![]() 处时,发现在
处时,发现在![]() 的北偏东
的北偏东![]() 方向,相距
方向,相距![]() 海里处的
海里处的![]() 点有一可疑船只正沿
点有一可疑船只正沿![]() 方向行驶,
方向行驶,![]() 点在
点在![]() 港口的北偏东
港口的北偏东![]() 方向上,海监船向
方向上,海监船向![]() 港口发出指令,执法船立即从
港口发出指令,执法船立即从![]() 港口沿
港口沿![]() 方向驶出,在
方向驶出,在![]() 处成功拦截可疑船只,此时
处成功拦截可疑船只,此时![]() 点与
点与![]() 点的距离为
点的距离为![]() 海里.
海里.
(1)求![]() 的度数与
的度数与![]() 点到直线
点到直线![]() 的距离;
的距离;
(2)执法船从![]() 到
到![]() 航行了多少海里?(结果保留根号)
航行了多少海里?(结果保留根号)
查看答案和解析>>
科目: 来源: 题型:
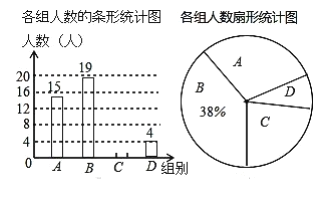
【题目】近年来我市大力发展绿色交通,构建公共、绿色交通体系,将“共享单车”陆续放置在人口流量较大的地方,琪琪同学随机调查了若干市民租用“共享单车”的骑车时间![]() (单位:分),将获得的数据分成四组,绘制了如下统计图(
(单位:分),将获得的数据分成四组,绘制了如下统计图(![]() ),根据图中信息,解答下列问题:
),根据图中信息,解答下列问题:
(1)这项被调查的总人数是 人,表示![]() 组的扇形统计图的圆心角的度数为 .
组的扇形统计图的圆心角的度数为 .
(2)若某小区共有![]() 人,根据调查结果,估计租用“共享单车”的骑车时间为
人,根据调查结果,估计租用“共享单车”的骑车时间为![]() 的大约有多少人?
的大约有多少人?
(3)如果琪琪同学想从![]() 组的甲、乙、丙、丁四人中随机选择两人了解平时租用“共享单车”的骑车时间情况,请用列表或画树状图的方法求出恰好选中甲的概率.
组的甲、乙、丙、丁四人中随机选择两人了解平时租用“共享单车”的骑车时间情况,请用列表或画树状图的方法求出恰好选中甲的概率.
查看答案和解析>>
科目: 来源: 题型:
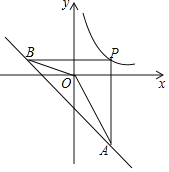
【题目】如图,P为反比例函数y=![]() (k>0)在第一象限内图象上的一点,过点P分别作x轴,y轴的垂线交一次函数y=﹣x﹣4的图象于点A、B.若∠AOB=135°,则k的值是( )
(k>0)在第一象限内图象上的一点,过点P分别作x轴,y轴的垂线交一次函数y=﹣x﹣4的图象于点A、B.若∠AOB=135°,则k的值是( )
A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
科目: 来源: 题型:
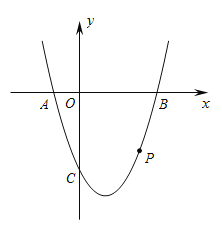
【题目】如图,抛物线![]() 与x轴相交于
与x轴相交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴相交于点
轴相交于点![]() .
.![]() 为抛物线上一点,横坐标为
为抛物线上一点,横坐标为![]() ,且
,且![]() .
.
⑴求此抛物线的解析式;
⑵当点![]() 位于
位于![]() 轴下方时,求
轴下方时,求![]() 面积的最大值;
面积的最大值;
⑶设此抛物线在点![]() 与点
与点![]() 之间部分(含点
之间部分(含点![]() 和点
和点![]() )最高点与最低点的纵坐标之差为
)最高点与最低点的纵坐标之差为![]() .
.
①求![]() 关于
关于![]() 的函数解析式,并写出自变量
的函数解析式,并写出自变量![]() 的取值范围;
的取值范围;
②当![]() 时,直接写出
时,直接写出![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com