练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

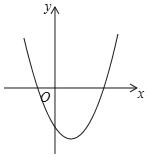
    【题目】如图，在平直角坐标系中，O为坐标原点，抛物线y=x2﹣mx﹣1的对称轴为直线x=1．若关于x的一元二次方程x2﹣mx﹣1﹣n=0(n为实数)在0＜x＜3的范围内有解，则n的取值范围是______．

    【答案】﹣2≤n＜2．

    【解析】

    根据给出的对称轴求出函数解析式为y=x2﹣2x﹣1，将一元二次方程x2﹣mx﹣1﹣n=0的实数根可以看做y=x2﹣2x﹣1与函数y=n的有交点，再由0＜x＜3的范围确定y的取值范围即可求解．

    解：∵抛物线y=x2﹣mx﹣1的对称轴为直线x=1，

    ∴m=2，

    ∴y=x2﹣2x﹣1，

    ∴一元二次方程x2﹣mx﹣1﹣n=0的实数根可以看做y=x2﹣2x﹣1与函数y=n的有交点．

    ∵方程在0＜x＜3的范围内有实数根，

    当x=0时，y=﹣1；

    当x=3时，y=2；

    函数y=x2﹣2x﹣1在x=1时有最小值﹣2；

    ∴﹣2≤n＜2．

    故答案为：﹣2≤n＜2．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某化工厂要在规定时间内搬运1200吨化工原料．现有，两种机器人可供选择，已知型机器人比型机器人每小时多搬运30吨型，机器人搬运900吨所用的时间与型机器人搬运600吨所用的时间相等．

    (1)求两种机器人每小时分别搬运多少吨化工原料．

    (2)该工厂原计划同时使用这两种机器人搬运，工作一段时间后，型机器人又有了新的搬运任务需离开，但必须保证这批化工原料在11小时内全部搬运完毕．问型机器人至少工作几个小时，才能保证这批化工原料在规定的时间内完成？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图矩形COAB，点B（4，3），点H位于边BC上．

    直线l1：2x﹣y+3＝0

    直线l2：2x﹣y﹣3＝0

    （1）若点N为l2上第一象限的点，△AHN为等腰Rt△，求N坐标．

    （2）若把l1、l2上的点构成的图形称为图形V．已知矩形AJHI的顶点J在图形V上，I为平面系上的点，且J（x，y），求x的范围（写出过程）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】学了一元二次方程的根与系数的关系后，小亮兴奋地说：“若设一元二次方程的两个根为，由根与系数的关系有，，由此就能快速求出，，···的值了． 比如设是方程的两个根，则，，得．

    小亮的说法对吗？简要说明理由；

    写一个你最喜欢的元二次方程，并求出两根的平方和；

    已知是关于的方程的一个根，求方程的另一个根与的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

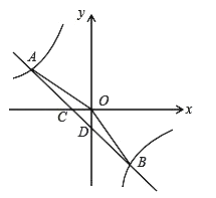
    【题目】如图，在平面直角坐标系中，一次函数的图象与反比例函数的图象交于第二、四象限内的两点，与轴交于点，与轴交于点，点的坐标是，连接，且．

    （1）求这个反比例函数和一次函数的解析式；

    （2）根据图象，直接写出不等式的解集．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】周末，小明匀速步行去省图书馆看书，当出发15min后距家1800m时，爸爸驾车匀速从家沿相同路线追赶小明，追上小明后，二人驾车继续按原速前行到达图书馆，小明留在图书馆看书，爸爸驾车继续按原速去单位办事设小明与爸爸之间的路程y(m)与小明出发的时间x(min)之间的函数图象如图所示．

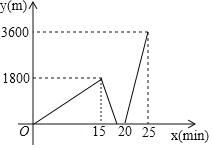
    （1）小明步行速度是 m/min，爸爸驾车速度是 m/min；

    （2）当爸爸从省图书馆到单位时，求y与x之间的函数关系式；

    （3）当爸爸与省图书馆之间的路程为2160m时，直接写出爸爸驾车行驶的时间．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

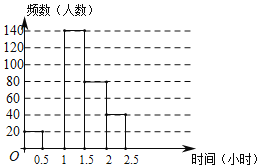
    【题目】某区规定学生每天户外体育活动时间不少于1小时，为了解学生参加户外体育活动的情况，对部分学生每天参加户外体育活动的时间进行了随机抽样调查，并将调查结果绘制成如图的统计图表（不完整）．请根据图表中的信息，解答下列问题：

    （1）表中的a＝_____，将频数分布直方图补全；

    （2）该区8000名学生中，每天户外体育活动的时间不足1小时的学生大约有多少名？

    （3）若从参加户外体育活动时间最长的3名男生和1名女生中随机抽取两名，请用画树状图或列表法求恰好抽到1名男生和1名女生的概率．

    组别

    时间（小时）

    频数（人数）

    频率

    A

    0≤t＜0.5

    20

    0.05

    B

    0.5≤t＜1

    a

    0.3

    C

    l≤t＜1.5

    140

    0.35

    D

    1.5≤t＜2

    80

    0.2

    E

    2≤t＜2.5

    40

    0.1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有甲、乙两个不透明的布袋，甲袋中有3个完全相同的小球，分别标有数字0，1和2；乙袋中有3个完全相同的小球，分别标有数字1，2和3，小明从甲袋中随机取出1个小球，记录标有的数字为x，再从乙袋中随机取出1个小球，记录标有的数字为y，这样确定了点M的坐标(x，y)．

    （1）写出点M所有可能的坐标；

    （2）求点M在直线上的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，一次函数y＝kx+b（k≠0）的图象与反比例函数的图象交于点C（n，3），与x轴、y轴分别交于点A、B，过点C作CM⊥x轴，垂足为M．若，OA＝2.

    （1）求反比例函数和一次函数的解析式；

    （2）当kx+b﹣＞0时，求x的取值范围．

    查看答案和解析>>

    同步练习册答案