
【题目】周末,小明匀速步行去省图书馆看书,当出发15min后距家1800m时,爸爸驾车匀速从家沿相同路线追赶小明,追上小明后,二人驾车继续按原速前行到达图书馆,小明留在图书馆看书,爸爸驾车继续按原速去单位办事设小明与爸爸之间的路程y(m)与小明出发的时间x(min)之间的函数图象如图所示.
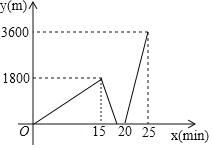
(1)小明步行速度是 m/min,爸爸驾车速度是 m/min;
(2)当爸爸从省图书馆到单位时,求y与x之间的函数关系式;
(3)当爸爸与省图书馆之间的路程为2160m时,直接写出爸爸驾车行驶的时间.
【答案】(1)120;720;(2)y=720x﹣1440;(3)2min或8min.
【解析】
(1)根据“速度=路程÷时间”解答即可;
(2)利用待定系数法解答即可;
(3)根据爸爸驾车速度求出小明家到图书馆的距离,即可求出当爸爸与省图书馆之间的路程为2160m时,爸爸驾车行驶的时间.
解:(1)小明步行速度是:1800÷15=120(m/min),
爸爸驾车速度是:3600÷(25﹣20)=720(m/min).
故答案为:120;720;
(2)设y与x之间的函数关系式为y=kx+b,根据题意得
![]() ,
,
解得:![]() ,
,
∴y与x之间的函数关系式为:y=720x﹣1440;
(3)小明家到图书馆的距离为:720×(20﹣15)=3600(m),
(3600﹣2160)÷720=2(min),(3600+2160)÷720=8(min),
答:当爸爸与省图书馆之间的路程为2160m时,爸爸驾车行驶的时间为2min或8min.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=8厘米,AC=16厘米,点P从A出发,以每秒2厘米的速度向B运动,点Q从C同时出发,以每秒3厘米的速度向A运动,其中一个动点到端点时,另一个动点也相应停止运动,那么,当以A、P、Q为顶点的三角形与△ABC相似时,运动时间为_________________
|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=-x2+bx+c的图象经过A(-2,-1),B(0,7)两点.
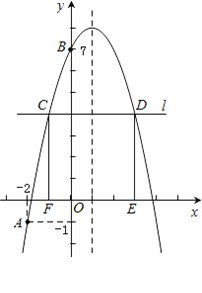
(1)求该抛物线的解析式及对称轴;
(2)当x为何值时,y>0?
(3)在x轴上方作平行于x轴的直线l,与抛物线交于C,D两点(点C在对称轴的左侧),过点C,D作x轴的垂线,垂足分别为F,E.当矩形CDEF为正方形时,求C点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
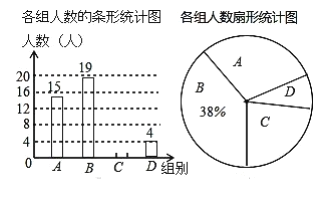
【题目】近年来我市大力发展绿色交通,构建公共、绿色交通体系,将“共享单车”陆续放置在人口流量较大的地方,琪琪同学随机调查了若干市民租用“共享单车”的骑车时间![]() (单位:分),将获得的数据分成四组,绘制了如下统计图(
(单位:分),将获得的数据分成四组,绘制了如下统计图(![]() ),根据图中信息,解答下列问题:
),根据图中信息,解答下列问题:
(1)这项被调查的总人数是 人,表示![]() 组的扇形统计图的圆心角的度数为 .
组的扇形统计图的圆心角的度数为 .
(2)若某小区共有![]() 人,根据调查结果,估计租用“共享单车”的骑车时间为
人,根据调查结果,估计租用“共享单车”的骑车时间为![]() 的大约有多少人?
的大约有多少人?
(3)如果琪琪同学想从![]() 组的甲、乙、丙、丁四人中随机选择两人了解平时租用“共享单车”的骑车时间情况,请用列表或画树状图的方法求出恰好选中甲的概率.
组的甲、乙、丙、丁四人中随机选择两人了解平时租用“共享单车”的骑车时间情况,请用列表或画树状图的方法求出恰好选中甲的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平直角坐标系中,O为坐标原点,抛物线y=x2﹣mx﹣1的对称轴为直线x=1.若关于x的一元二次方程x2﹣mx﹣1﹣n=0(n为实数)在0<x<3的范围内有解,则n的取值范围是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一道习题:如图1,已知OA和OB是⊙O的半径,并且OA⊥OB,P是OA上任一点(不与O、A重合),BP的延长线交⊙O于Q,过Q点作⊙O的切线交OA的延长线于R.
(1)证明:RP=RQ;
(2)请探究下列变化:
A、变化一:交换题设与结论.已知:如图1,OA和OB是⊙O的半径,并且OA⊥OB,P是OA上任一点(不与O、A重合),BP的延长线交⊙O于Q,R是OA的延长线上一点,且RP=RQ.证明:RQ为⊙O的切线.

B、变化二:运动探求. ①如图2,若OA向上平移,变化一中结论还成立吗?(只交待判断) 答:_________.
②如图3,如果P在OA的延长线上时,BP交⊙O于Q,过点Q作⊙O的切线交OA的延长线于R,原题中的结论还成立吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=x+2与反比例函数y2=![]() 的图象交于A,B两点,点A的坐标为(1,a).
的图象交于A,B两点,点A的坐标为(1,a).
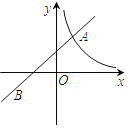
(1)求出k的值及点B的坐标;
(2)根据图象,写出y1>y2时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
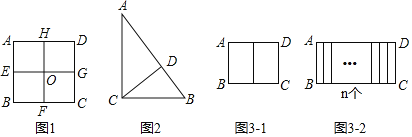
【题目】阅读下列材料,完成任务:
自相似图形,定义:若某个图形可分割为若干个都与它相似的图形,则称这个图形是自相似图形.例如:正方形ABCD中,点E、F、G、H分别是AB、BC、CD、DA边的中点,连接EG,HF交于点O,易知分割成的四个四边形AEOH、EBFO、OFCG、HOGD均为正方形,且与原正方形相似,故正方形是自相似图形.
(1)图1中正方形ABCD分割成的四个小正方形中,每个正方形与原正方形的相似比为______;
(2)如图2,已知△ABC中,∠ACB=90°,AC=4,BC=3,小明发现△ABC也是“自相似图形”,他的思路是:过点C作CD⊥AB于点D,则CD将△ABC分割成2个与它自己相似的小直角三角形.则△ACD与△ABC的相似比为_____;则△BCD与△ABC的相似比为_____;
(3)现有一个矩形ABCD是自相似图形,其中长AD=a,宽AB=b(a>b).
①如图3﹣1,若将矩形ABCD纵向分割成两个全等矩形,且与原矩形都相似,则a=_____(用含b的式子表示):
②如图3﹣2,若将矩形ABCD纵向分割成n个全等矩形,且与原矩形都相似,则a=______(用含n,b的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以AB边为直径的⊙O经过点P,C是⊙O上一点,连结PC交AB于点E,且∠ACP=60°,PA=PD.
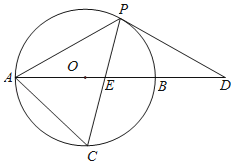
(1)试判断PD与⊙O的位置关系,并说明理由;
(2)若点C是弧AB的中点,已知AB=2,求CECP的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com