
【题目】阅读下列材料,完成任务:
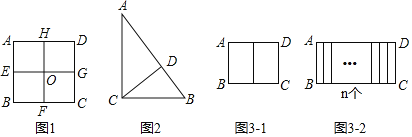
自相似图形,定义:若某个图形可分割为若干个都与它相似的图形,则称这个图形是自相似图形.例如:正方形ABCD中,点E、F、G、H分别是AB、BC、CD、DA边的中点,连接EG,HF交于点O,易知分割成的四个四边形AEOH、EBFO、OFCG、HOGD均为正方形,且与原正方形相似,故正方形是自相似图形.
(1)图1中正方形ABCD分割成的四个小正方形中,每个正方形与原正方形的相似比为______;
(2)如图2,已知△ABC中,∠ACB=90°,AC=4,BC=3,小明发现△ABC也是“自相似图形”,他的思路是:过点C作CD⊥AB于点D,则CD将△ABC分割成2个与它自己相似的小直角三角形.则△ACD与△ABC的相似比为_____;则△BCD与△ABC的相似比为_____;
(3)现有一个矩形ABCD是自相似图形,其中长AD=a,宽AB=b(a>b).
①如图3﹣1,若将矩形ABCD纵向分割成两个全等矩形,且与原矩形都相似,则a=_____(用含b的式子表示):
②如图3﹣2,若将矩形ABCD纵向分割成n个全等矩形,且与原矩形都相似,则a=______(用含n,b的式子表示).
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ;(3)①
;(3)①![]() b;②
b;②![]() b.
b.
【解析】
(1)先得出AH=![]() AD,然后进一步即可得出结论;
AD,然后进一步即可得出结论;
(2)根据勾股定理求出AB,然后通过相似三角形性质进一步求解即可得出结论;
(3)①根据矩形ABEF∽矩形FECD得出比例式即可得出结论;②同①的方法即可得出结论;
(1)∵点H是AD的中点,
∴AH=![]() AD,
AD,
∵正方形AEOH∽正方形ABCD,
∴相似比为:![]() ;
;
故答案为:![]() ;
;
(2)在Rt△ABC中,AC=4,BC=3,根据勾股定理得,AB=5,
∴△ACD与△ABC相似的相似比为:![]() ,△BCD与△ABC的相似比为:
,△BCD与△ABC的相似比为:![]() ,
,
故答案为:![]() ,
,![]() ;
;
(3)①∵矩形ABEF∽矩形FECD,
∴AF:AB=AB:AD,
即![]() a:b=b:a,
a:b=b:a,
∴a=![]() b;
b;
故答案为:![]() b
b
②每个小矩形都是全等的,则其边长为b和![]() a,
a,
则b:![]() a=a:b,
a=a:b,
∴a=![]() b;
b;
故答案为:![]() b
b


科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,点E是边AB的中点,点O是线段AE上的一个动点(不与A、E重合),以O为圆心,OB为半径的圆与边AD相交于点M,过点M作⊙O的切线交DC于点N,连接OM、ON、BM、BN.记△MNO、△AOM、△DMN的面积分别为S1、S2、S3,则下列结论不一定成立的是( )
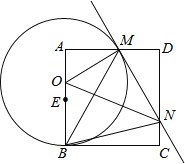
A.S1>S2+S3 B.△AOM∽△DMN C.∠MBN=45° D.MN=AM+CN
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小明匀速步行去省图书馆看书,当出发15min后距家1800m时,爸爸驾车匀速从家沿相同路线追赶小明,追上小明后,二人驾车继续按原速前行到达图书馆,小明留在图书馆看书,爸爸驾车继续按原速去单位办事设小明与爸爸之间的路程y(m)与小明出发的时间x(min)之间的函数图象如图所示.
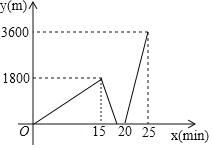
(1)小明步行速度是 m/min,爸爸驾车速度是 m/min;
(2)当爸爸从省图书馆到单位时,求y与x之间的函数关系式;
(3)当爸爸与省图书馆之间的路程为2160m时,直接写出爸爸驾车行驶的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.“概率为0.0001的事件”是不可能事件
B.任意掷一枚质地均匀的硬币10次,正面向上的一定是5次
C.“任意画出一个等边三角形,它是轴对称图形”是随机事件
D.“任意画出一个平行四边行,它是中心对称图形”是必然事件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两个不透明的布袋,甲袋中有3个完全相同的小球,分别标有数字0,1和2;乙袋中有3个完全相同的小球,分别标有数字1,2和3,小明从甲袋中随机取出1个小球,记录标有的数字为x,再从乙袋中随机取出1个小球,记录标有的数字为y,这样确定了点M的坐标(x,y).
(1)写出点M所有可能的坐标;
(2)求点M在直线![]() 上的概率.
上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC中,底边BC长为8,腰长为6,点D是BC边上一点,过点B作AC的平行线与过A、B、D三点的圆交于点E,连接DE,则DE的最小值是___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程或方程组解应用题:
去年暑期,某地由于暴雨导致电路中断,该地供电局组织电工进行抢修.供电局距离抢修工地15千米.抢修车装载着所需材料先从供电局出发,10分钟后,电工乘吉普车从同一地点出发,结果他们同时到达抢修工地.已知吉普车速度是抢修车速度的1.5倍,求吉普车的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,AB=AC,D为BC的中点,以D为顶点作∠MDN=∠B,
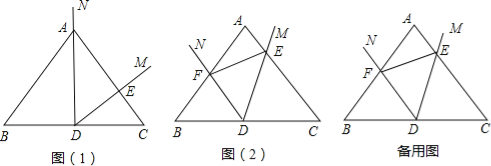
(1)如图(1)当射线DN经过点A时,DM交AC边于点E,不添加辅助线,写出图中所有与△ADE相似的三角形.
(2)如图(2),将∠MDN绕点D沿逆时针方向旋转,DM,DN分别交线段AC,AB于E,F点(点E与点A不重合),不添加辅助线,写出图中所有的相似三角形,并证明你的结论.
(3)在图(2)中,若AB=AC=10,BC=12,当△DEF的面积等于△ABC的面积的![]() 时,求线段EF的长.
时,求线段EF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com