
【题目】二次函数![]() 的图像如图所示,下列结论正确是( )
的图像如图所示,下列结论正确是( )
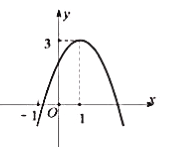
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]() 有两个不相等的实数根
有两个不相等的实数根
【答案】C
【解析】观察图象:开口向下得到a<0;对称轴在y轴的右侧得到a、b异号,则b>0;抛物线与y轴的交点在x轴的上方得到c>0,所以abc<0;由对称轴为x=![]() =1,可得2a+b=0;当x=-1时图象在x轴下方得到y=a-b+c<0,结合b=-2a可得 3a+c<0;观察图象可知抛物线的顶点为(1,3),可得方程
=1,可得2a+b=0;当x=-1时图象在x轴下方得到y=a-b+c<0,结合b=-2a可得 3a+c<0;观察图象可知抛物线的顶点为(1,3),可得方程![]() 有两个相等的实数根,据此对各选项进行判断即可.
有两个相等的实数根,据此对各选项进行判断即可.
观察图象:开口向下得到a<0;对称轴在y轴的右侧得到a、b异号,则b>0;抛物线与y轴的交点在x轴的上方得到c>0,所以abc<0,故A选项错误;
∵对称轴x=![]() =1,∴b=-2a,即2a+b=0,故B选项错误;
=1,∴b=-2a,即2a+b=0,故B选项错误;
当x=-1时, y=a-b+c<0,又∵b=-2a,∴ 3a+c<0,故C选项正确;
∵抛物线的顶点为(1,3),
∴![]() 的解为x1=x2=1,即方程有两个相等的实数根,故D选项错误,
的解为x1=x2=1,即方程有两个相等的实数根,故D选项错误,
故选C.


科目:初中数学 来源: 题型:
【题目】如图,直线l1解析式为y=x+2,且与坐标轴分别交于A、B两点,与双曲线交于点P(﹣1,1).点M是双曲线在第四象限上的一点,过点M的直线l2与双曲线只有一个公共点,并与坐标轴分别交于点C、点D,当四边形ABCD的面积取最小值时,则点M的坐标为( )
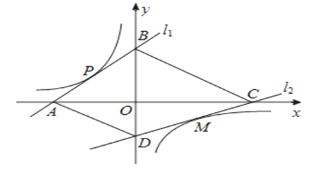
A. (1,﹣1) B. (2,﹣![]() ) C. (3,﹣
) C. (3,﹣![]() ) D. 不能确定
) D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,∠ACB=90°,OC=2BO,AC=6,点B的坐标为(1,0),抛物线y=﹣x2+bx+c经过A、B两点.
(1)求点A的坐标;
(2)求抛物线的解析式;
(3)点P是直线AB上方抛物线上的一点,过点P作PD垂直x轴于点D,交线段AB于点E,使PE=![]() DE.
DE.
①求点P的坐标;
②在直线PD上是否存在点M,使△ABM为直角三角形?若存在,求出符合条件的所有点M的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB和抛物线的交点是A(0,-3),B(5,9),已知抛物线的顶点D的横坐标是2.

(1)求抛物线的解析式及顶点坐标;
(2)在![]() 轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)在直线AB的下方抛物线上找一点P,连接PA,PB使得△PAB的面积最大,并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图抛物线y=ax2+bx+c的对称轴是x=﹣1,与x轴的一个交点为(﹣5,0),则一元二次方程ax2+bx+c=0的另一根为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y1=﹣x2+mx+n,直线y2=kx+b,y1的对称轴与y2交于点A(﹣1,5),点A与y1的顶点B的距离是4.
(1)求y1的解析式;
(2)若y2随着x的增大而增大,且y1与y2都经过x轴上的同一点,求y2的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y1=x2+mx+n,直线y2=2x+1,抛物线y1的对称轴与直线y2的交点为点A,且点A的纵坐标为5.
(1)求m的值;
(2)若点A与抛物线y1的顶点B的距离为4,求抛物线y1的解析式;
(3)若抛物线y1与直线y2只有一个公共点,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从A,B两题中任选一题解答,我选择________.
A.如图(1)是两棵树在同一盏路灯下的影子.
(1)确定该路灯泡所在的位置;
(2)如果此时小颖所在位置恰好与这两棵树所在的位置共线(三点在一条直线上),请画出图中表示小颖影子的线段AB.
B.如图(2),小明从点A出发沿AB方向匀速前进,2秒后到达点D,此时他在某一灯光下的影子为DA,继续按此速度行走2秒到达点F,此时他在同一灯光下的影子落在其身后的线段DF上,测得此时影长MF为1.2米,然后他将速度提高到原来的1.5倍,再行走2秒到达点H.他在同一灯光下的影子恰好是HB.图中线段CD,EF,GH表示小明的身高.

(1)请在图中画出小明的影子MF;
(2)若A、B两地相距12米,则小明原来的速度为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小美周末来到公园,发现在公园一角有一种“守株待兔”游戏.游戏设计者提供了一只兔子和一个有A、B、C、D、E五个出入口的兔笼,而且笼内的兔子从每个出入口走出兔笼的机会是均等的.规定:
①玩家只能将小兔从A、B两个出入口放入;
②如果小兔进入笼子后选择从开始进入的出入口离开,则可获得一只价值5元小兔玩具,否则应付费3元.
(1)问小美得到小兔玩具的机会有多大?
(2)假设有100人次玩此游戏,估计游戏设计者可赚多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com