
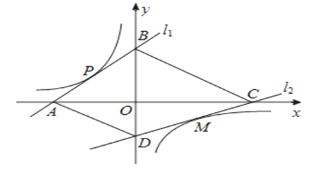
【题目】如图,直线l1解析式为y=x+2,且与坐标轴分别交于A、B两点,与双曲线交于点P(﹣1,1).点M是双曲线在第四象限上的一点,过点M的直线l2与双曲线只有一个公共点,并与坐标轴分别交于点C、点D,当四边形ABCD的面积取最小值时,则点M的坐标为( )
A. (1,﹣1) B. (2,﹣![]() ) C. (3,﹣
) C. (3,﹣![]() ) D. 不能确定
) D. 不能确定
【答案】A
【解析】
先求出A、B两点的坐标,有P(﹣1,1)在反比例函数图象上求得解析式为y![]() ,设M点横坐标为a,进而可得M点坐标(a,
,设M点横坐标为a,进而可得M点坐标(a,![]() );再设直线l2的解析式为y=bx+c,根据条件“过点M的直线l2与双曲线只有一个公共点”,将M点坐标代入直线l2的解析式,求得用a表示的C、D两点坐标.由A、B、C、D四点坐标,可得AC、BD的长,因为AC⊥BD,有S四边形ABCD
);再设直线l2的解析式为y=bx+c,根据条件“过点M的直线l2与双曲线只有一个公共点”,将M点坐标代入直线l2的解析式,求得用a表示的C、D两点坐标.由A、B、C、D四点坐标,可得AC、BD的长,因为AC⊥BD,有S四边形ABCD![]() ACBD,据此得到一个关于a的式子,通过化简、配方即可求得S四边形ABCD的最小值,故可得出a的值,由此得出结论.
ACBD,据此得到一个关于a的式子,通过化简、配方即可求得S四边形ABCD的最小值,故可得出a的值,由此得出结论.
∵直线l1解析式为y=x+2,且与坐标轴分别交于A、B两点,∴A(﹣2,0),B(0,2).
设反比例函数的解析式为y![]() .
.
∵点P(﹣1,1)在反比例函数y![]() 的图象上,∴k=xy=﹣1,∴反比例函数的解析式为y
的图象上,∴k=xy=﹣1,∴反比例函数的解析式为y![]() .
.
∵点M在第四象限,且在反比例函数y![]() 的图象上,∴可设点M的坐标为(a,
的图象上,∴可设点M的坐标为(a,![]() ),其中a>0.
),其中a>0.
设直线l2的解析式为y=bx+c,则ab+c![]() ,∴c
,∴c![]() ab,∴y=bx
ab,∴y=bx![]() ab.
ab.
∵直线y=bx![]() ab与双曲线y
ab与双曲线y![]() 只有一个交点,∴方程bx
只有一个交点,∴方程bx![]() ab
ab![]() 即bx2﹣(
即bx2﹣(![]() ab)x+1=0有两个相等的实根,∴[﹣(
ab)x+1=0有两个相等的实根,∴[﹣(![]() ab)]2﹣4b=(
ab)]2﹣4b=(![]() ab)2﹣4b=(
ab)2﹣4b=(![]() ab)2=0,∴
ab)2=0,∴![]() ab,∴b
ab,∴b![]() ,c
,c![]() ,∴直线l2的解析式为y
,∴直线l2的解析式为y![]() ,∴当x=0时,y
,∴当x=0时,y![]() ,则点D的坐标为(0,
,则点D的坐标为(0,![]() );
);
当y=0时,x=2a,则点C的坐标为(2a,0),∴AC=2a﹣(﹣2)=2a+2,BD=2﹣(![]() )=2
)=2![]() .
.
∵AC⊥BD,∴S四边形ABCD![]() ACBD
ACBD![]() (2a+2)(2
(2a+2)(2![]() )=4+2(a
)=4+2(a![]() )=4+2[(
)=4+2[(![]() )2+2]
)2+2]
=8+2(![]() )2.
)2.
∵(![]() )2≥0,∴S四边形ABCD≥8,∴当且仅当(
)2≥0,∴S四边形ABCD≥8,∴当且仅当(![]() )2=0,即a=1时,四边形有最小值,∴M(1,﹣1).
)2=0,即a=1时,四边形有最小值,∴M(1,﹣1).
故选A.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 旋转,边
旋转,边![]() 分别交边
分别交边![]() 、
、![]() 于
于![]() 、
、![]() 两点.
两点.
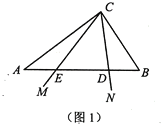

(1)若![]() ,
,![]() ,求
,求![]() 的最小值;
的最小值;
(2)如图2,设![]() ,点
,点![]() 是
是![]() 的中点,连接
的中点,连接![]() ,当
,当![]() 旋转到
旋转到![]() 与
与![]() 的交点
的交点![]() 是
是![]() 的中点时,过点
的中点时,过点![]() 作
作![]() 的垂线交CM于点
的垂线交CM于点![]() ,连接
,连接![]() 、
、![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCO放在直角坐标系中,其中顶点B的坐标为(10, 8),E是BC边上一点将△ABE沿AE折叠,点B刚好与OC边上点D重合,过点E的反比例函数y=![]() 的图象与边AB交于点F, 则线段AF的长为( )
的图象与边AB交于点F, 则线段AF的长为( )

A. ![]() B. 2 C.
B. 2 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十九大”报告提出了我国将加大治理环境污染的力度,还我青山绿水,其中雾霾天气让环保和健康问题成为焦点,为了调查学生对雾霾天气知识的了解程度,某校在全校学生中抽取400名同学做了一次调查,根据调查统计结果,绘制了不完整的一种统计图表.
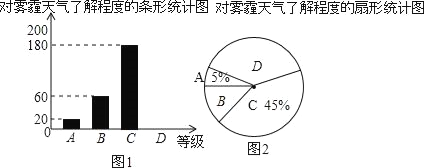
对雾霾了解程度的统计表
对雾霾的了解程度 | 百分比 |
A.非常了解 | 5% |
B.比较了解 | m |
C.基本了解 | 45% |
D.不了解 | n |
请结合统计图表,回答下列问题:
(1)统计表中:m= ,n= ;
(2)请在图1中补全条形统计图;
(3)请问在图2所示的扇形统计图中,D部分扇形所对应的圆心角是多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一垂直于地面的灯柱AB被一钢筋CD固定,CD与地面成45°夹角(∠CDB=45°),在C点上方2米处加固另一条钢线ED,ED与地面成53°夹角(∠EDB=53°),那么钢线ED的长度约为多少米?(结果精确到1米,参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】去学校食堂就餐,经常会在一个买菜窗口前等待,经调查发现,同学的舒适度指数y与等时间x(分)之间满足反比例函数关系,如下表:
等待时间x | 1 | 2 | 5 | 10 | 20 |
舒适度指数y | 100 | 50 | 20 | 10 | 5 |
已知学生等待时间不超过30分钟
(1)求y与x的函数关系式,并写出自变量x的取值范围.
(2)若等待时间8分钟时,求舒适度的值;
(3)舒适度指数不低于10时,同学才会感到舒适.请说明,作为食堂的管理员,让每个在窗口买菜的同学最多等待多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是⊙O的内接四边形,AC为直径,点B是弧AC的中点,若AC=7,BD=6,则由四个弓形组成的阴影部分的面积为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
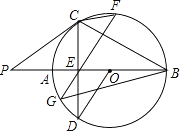
【题目】已知:如图,AB是⊙O的直径,点P在BA的延长线上,弦CD交AB于E,连接OD、PC、BC,∠AOD=2∠ABC,∠P=∠D,过E作弦GF⊥BC交圆与G、F两点,连接CF、BG.则下列结论:①CD⊥AB;②PC是⊙O的切线;③OD∥GF;④弦CF的弦心距等于![]() BG.则其中正确的是( )
BG.则其中正确的是( )
A. ①②④ B. ③④ C. ①②③ D. ①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com