
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 旋转,边
旋转,边![]() 分别交边
分别交边![]() 、
、![]() 于
于![]() 、
、![]() 两点.
两点.
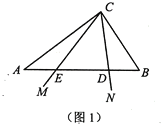

(1)若![]() ,
,![]() ,求
,求![]() 的最小值;
的最小值;
(2)如图2,设![]() ,点
,点![]() 是
是![]() 的中点,连接
的中点,连接![]() ,当
,当![]() 旋转到
旋转到![]() 与
与![]() 的交点
的交点![]() 是
是![]() 的中点时,过点
的中点时,过点![]() 作
作![]() 的垂线交CM于点
的垂线交CM于点![]() ,连接
,连接![]() 、
、![]() ,求证:
,求证:![]() .
.
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:
【题目】现有两组相同的扑克牌,每组两张,两张牌的牌面数字分别是2和3,从每组牌中各随机摸出一张牌,称为一次试验.
(1)小红与小明用一次试验做游戏,如果摸到的牌面数字相同小红获胜,否则小明获胜,请用列表法或画树状图的方法说明这个游戏是否公平?
(2)小丽认为:“在一次试验中,两张牌的牌面数字和可能为4、5、6三种情况,所以出现‘和为4’的概率是![]() ”,她的这种看法是否正确?说明理由.
”,她的这种看法是否正确?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 是第一、三象限的角平分线.
是第一、三象限的角平分线.

(1)由图观察易知A(0,2)关于直线l的对称点A′的坐标为(2,0),请在图中分别标明B(5,3)、C(-2,5)关于直线l的对称点B′、C′的位置,并写出他们的坐标:![]() ___________、
___________、![]() ___________;
___________;
(2)结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点![]() 关于第一、三象限的角平分线
关于第一、三象限的角平分线![]() 的对称点
的对称点![]() 的坐标为___________(不必证明);
的坐标为___________(不必证明);
(3)已知两点![]() 、
、![]() ,试在直线L上画出点Q,使点Q到D、E两点的距离之和最小,求QD+QE的最小值.
,试在直线L上画出点Q,使点Q到D、E两点的距离之和最小,求QD+QE的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在坡顶A处的同一水平面上有一座大型纪念碑BC,某同学在斜坡底P处测得该碑的碑顶B的仰角为45°,然后他们沿着坡度为1:2.4的斜坡AP攀行了26米到达坡顶A,在坡顶A处又测得该碑的碑顶B的仰角为76°,求纪念碑BC的高度(结果精确到0.1米).(过点A作AD⊥PO,垂足为点D.坡度=AD:PD)(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
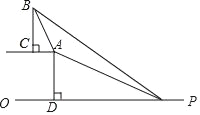
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司试销一种成本单价为50元/件的新产品,规定试销时销售单价不低于成本单价,又不高于80元/件,经试销调查,发现销售量y(件)与销售单价x(元/件)可近似看作一次函数y=kx+b的关系(如图所示)
(I)根据图象,求一次函数y=kx+b的解析式,并写出自变量x的取值范围;
(Ⅱ)该公司要想每天获得最大的利润,应把销售单价定为多少?最大利润值为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=![]() x与双曲线y=
x与双曲线y=![]() 交于A、B两点,且点A的横坐标为
交于A、B两点,且点A的横坐标为![]() .
.
(1)求k的值;
(2)若双曲线y=![]() 上点C的纵坐标为3,求△AOC的面积;
上点C的纵坐标为3,求△AOC的面积;
(3)在坐标轴上有一点M,在直线AB上有一点P,在双曲线y=![]() 上有一点N,若以O、M、P、N为顶点的四边形是有一组对角为60°的菱形,请写出所有满足条件的点P的坐标.
上有一点N,若以O、M、P、N为顶点的四边形是有一组对角为60°的菱形,请写出所有满足条件的点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,在下列代数式中(1)a+b+c>0;(2)﹣4a<b<﹣2a(3)abc>0;(4)5a﹣b+2c<0; 其中正确的个数为( )
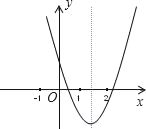
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1解析式为y=x+2,且与坐标轴分别交于A、B两点,与双曲线交于点P(﹣1,1).点M是双曲线在第四象限上的一点,过点M的直线l2与双曲线只有一个公共点,并与坐标轴分别交于点C、点D,当四边形ABCD的面积取最小值时,则点M的坐标为( )
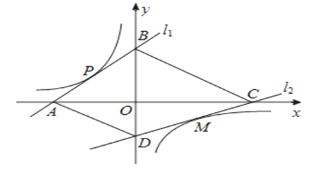
A. (1,﹣1) B. (2,﹣![]() ) C. (3,﹣
) C. (3,﹣![]() ) D. 不能确定
) D. 不能确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com