
【题目】已知关于 x 的函数 y=(m﹣1)x2+2x+m 图象与坐标轴只有 2 个交点,则m=_______.
【答案】1 或 0 或![]()
【解析】
分两种情况讨论:当函数为一次函数时,必与坐标轴有两个交点;
当函数为二次函数时,将(0,0)代入解析式即可求出m的值.
解:(1)当 m﹣1=0 时,m=1,函数为一次函数,解析式为 y=2x+1,与 x 轴
交点坐标为(﹣![]() ,0);与 y 轴交点坐标(0,1).符合题意.
,0);与 y 轴交点坐标(0,1).符合题意.
(2)当 m﹣1≠0 时,m≠1,函数为二次函数,与坐标轴有两个交点,则过原点,且与 x 轴有两个不同的交点,
于是△=4﹣4(m﹣1)m>0,
解得,(m﹣![]() )2<
)2<![]() ,
,
解得 m<![]() 或 m>
或 m>![]() .
.
将(0,0)代入解析式得,m=0,符合题意.
(3)函数为二次函数时,还有一种情况是:与 x 轴只有一个交点,与 Y 轴交于交于另一点,
这时:△=4﹣4(m﹣1)m=0,
解得:m=![]() .
.
故答案为:1 或 0 或![]() .
.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】(1)解方程x2﹣4x=12;
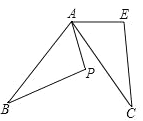
(2)如图,△ABP是由△ACE绕A点旋转得到的,若∠APB=110°,∠B=30°,∠PAC=20°,求旋转角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,⊙O是△ABC的外接圆,连接AO,若∠BAC+∠OAB=90°.
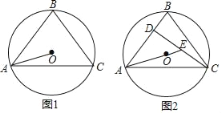
(1)求证:![]()
(2)如图2,作CD⊥AB交于D,AO的延长线交CD于E,若AO=3,AE=4,求线段AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
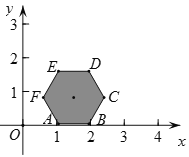
【题目】如图,在平面直角坐标xOy中,点A(1,0),B(2,0),正六边形ABCDEF沿x轴正方向无滑动滚动,每旋转60°为滚动1次,那么当正六边形ABCDEF滚动2017次时,点F的坐标是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
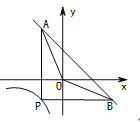
【题目】如图,P为反比例函数![]() (x<0)在第三象限内图象上的一点,过点P分别作x轴、y轴的垂线交一次函数y=-x+4的图像于点A、B.若AO、BO分别平分∠BAP,∠ABP ,则k的值为___________.
(x<0)在第三象限内图象上的一点,过点P分别作x轴、y轴的垂线交一次函数y=-x+4的图像于点A、B.若AO、BO分别平分∠BAP,∠ABP ,则k的值为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知矩形AOCB,AB=6cm,BC=16cm,动点P从点A出发,以3cm/s的速度向点O运动,直到点O为止;动点Q同时从点C出发,以2cm/s的速度向点B运动,与点P同时结束运动.
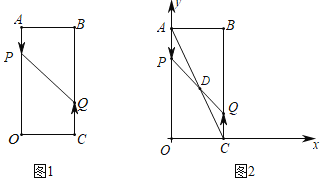
(1)当出发 时,点P和点Q之间的距离是10cm;
(2)逆向发散:当运动时间为2s时,P、Q两点的距离为 cm;当运动时间为4s时,P、Q两点的距离为 cm;
(3)探索发现:如图2,以点O为坐标原点,OC所在直线为x轴,OA所在直线为y轴,1cm长为单位长度建立平面直角坐标系,连接AC,与PQ相交于点D,若双曲线y=![]() 过点D,问k的值是否会变化?若会变化,说明理由;若不会变化,请求出k的值.
过点D,问k的值是否会变化?若会变化,说明理由;若不会变化,请求出k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】雅安地震牵动着全国人民的心,某单位开展了“一方有难,八方支援”赈灾捐款活动.第一天收到捐款10 000元,第三天收到捐款12 100元.
(1)如果第二天、第三天收到捐款的增长率相同,求捐款增长率;
(2)按照(1)中收到捐款的增长速度,第四天该单位能收到多少捐款?
查看答案和解析>>
科目:初中数学 来源: 题型:
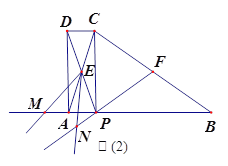
【题目】如图(1),在△ABC中,AB=BC,P为AB边上一点,连接CP,以PA、PC为邻边作![]() APCD,AC与PD相交于点E,已知∠ABC=∠AEP=
APCD,AC与PD相交于点E,已知∠ABC=∠AEP=![]() (0°<
(0°<![]() <90°).
<90°).
(1)求证: ∠EAP=∠EPA;
(2)![]() APCD是否为矩形?请说明理由;
APCD是否为矩形?请说明理由;
(3)如图(2),F为BC中点,连接FP,将∠AEP绕点E顺时针旋转适当的角度,得到∠MEN(点M、N分别是∠MEN的两边与BA、FP延长线的交点).猜想线段EM与EN之间的数量关系,并证明你的结论.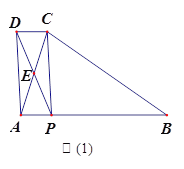
查看答案和解析>>
科目:初中数学 来源: 题型:
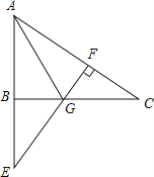
【题目】如图,在Rt△ABC中,∠ABC=90°,延长AB至E,使AE=AC,过E作EF⊥AC于F,EF交BC于G.
(1)求证:BE=CF;
(2)若∠E=40°,求∠AGB的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com