
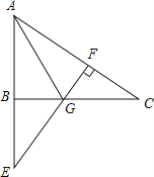
【题目】如图,在Rt△ABC中,∠ABC=90°,延长AB至E,使AE=AC,过E作EF⊥AC于F,EF交BC于G.
(1)求证:BE=CF;
(2)若∠E=40°,求∠AGB的度数.
【答案】(1)证明见解析;(2)∠AGB=65°.
【解析】
(1)首先证明△ABC![]() △AFE,推出AB=AF,即可解决问题.
△AFE,推出AB=AF,即可解决问题.
(2)在Rt△BEG中,∠BGE=90°-∠E=50°,推出∠BGF=130°,由Rt△AGF![]() Rt△AGB,推出∠AGB=∠AGF=
Rt△AGB,推出∠AGB=∠AGF=![]() ∠BGF即可解决问题.
∠BGF即可解决问题.
证明:(1)∵∠ABC=90°,EF⊥AC,
∴∠ABC=∠AFE=90°
在△AEF与△ACB中
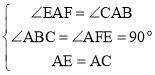 ,
,
∴△AEF![]() △ACB(AAS)
△ACB(AAS)
∴AF=AB,
∴BE=CF;
(2)∵△ABC![]() △AFE,
△AFE,
∴AB=AF,
在Rt△AGF和Rt△AGB中,
![]()
∴Rt△AFG![]() Rt△ABG(HL)
Rt△ABG(HL)
在Rt△BEG中,∠BGE=90°-∠E=50°,
∴∠BGF=130°,
∵Rt△AGF![]() Rt△AGB,
Rt△AGB,
∴∠AGB=∠AGF=![]() ∠BGF=65°.
∠BGF=65°.


科目:初中数学 来源: 题型:
【题目】已知⊙O 的直径为 4,AB 是⊙O 的弦,∠AOB=120°,点 P 在⊙O 上,若点 P到直线 AB 的距离为 1,则∠PAB 的度数为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
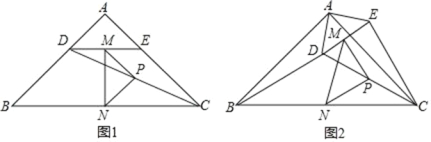
【题目】如图 1,在 Rt△ABC 中,∠A=90°,AB=AC,点 D、E 分别在边 AB、AC 上,AD=AE,连接DC,点 M、P、N 分别为 DE、DC、BC 的中点,
(1)观察猜想:如图 1 中,△PMN 是 三角形;
(2)探究证明:把△ADE 绕点 A 逆时针方向旋转到图 2 的位置,连接 MN,BD, CE.判断△PMN 的形状,并说明理由;
(3)拓展延伸:将△ADE 绕点 A 在平面内自由旋转,若 AD=4,AB=10,请求△PMN 面积的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
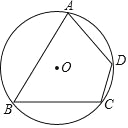
【题目】如图,已知四边形 ABCD 内接于⊙O,且已知∠ADC=120°;请仅用无刻度直尺作出一个30°的圆周角.要求:
(1)保留作图痕迹,写出作法,写明答案;
(2)证明你的作法的正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
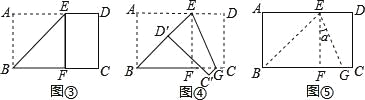
【题目】将长方形纸片 ABCD 沿过点 B 的直线折叠,使点 A 落在 BC 边上的点 F 处, 折痕为 BE(如图③);再沿过点 E 的直线折叠,使点 D 落在 BE 上的点处 D′,折痕为 EG(如图④);再展平纸片(如图⑤),则图⑤中∠α=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,对角线BD所在的直线上有两点E、F满足BE=DF,连接AE、AF、CE、CF,如图所示.
(1)求证:△ABE≌△ADF;
(2)试判断四边形AECF的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
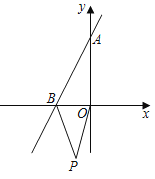
【题目】如图,直线y=2x+4分别与x轴,y轴交于B,A两点
(1)求△ABO的面积;
(2)如果在第三象限内有一点P(﹣1,m),请用含m的式子表示四边形AOPB的面积;
(3)在(2)的条件下,是否存在点P,使四边形AOPB的面积是△ABO面积的2倍?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com